正弦、余弦的诱导公式1 人教必修

总 课 题

三角函数

总课时

第 1 课时

课 题

正弦、余弦的诱导公式1

课 型

新授

教学目标

使学生掌握并会推导诱导公式一、二、三；

使学生能够学会利用诱导公式求三角函数值；能用公式进行化简；

渗透化归的思想

教学重点

诱导公式一、二、三

教学难点

诱导公式一、二、三的应用

教学过程

教学内容

备课札记

回忆诱导公式一，并说出有什么作用（可以把任意角的三角函数值，转化为0o到360o的角的三角函数值）

思考：对于0o到360o的角如何用α∈（0o,90o）来表示？

新知讲授：

α 当β∈

β= 180o-α 当β∈

180o＋α 当β∈

360o-α 当β∈

进行推广得到α为任意角的情况下也存在

利用三角函数线证明并推导诱导公式二

教学过程

教学内容

备课札记

给出诱导公式二：

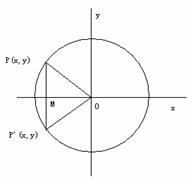
利用三角函数线证明并推导诱导公式三

给出诱导公式三：

例题讲授：

求下列三角函数值：

(1) cos225o 2)sin 3)sin4)cos(-240o)

例2.化简

例3.已知,求的值。

课堂练习：书p30T1T2T3T4

三、课堂小结：略

四、布置作业：另附

班级

高一（ ）

姓名

学号

课题

诱导公式1

一.选择题：

1. 下列各式中不正确的是 （ ）

A. B.

C.D.

2.已知角<的终边过点，则的值是 （ ）

A. B.C. D.

3.已知,且是第四象限的角，则的值是 （ ）

A. B.C.D.

4.若则的值为 （ ）

5.求值：

1）------______；2）=______; 3)=__________

6.已知,且θ为第三象限，则__________

7.已知, 则______________

8. 已知：, 求

1） 2)

9. 化简

10.设求的值。