椭圆第二定义的教学 人教选修
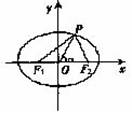现行高中《平面解析几何》课本对椭圆第二定义采用了从具体事例入手，引出一个新概念的定义的方法，这是数学教学中常用的从具体到抽象、从特殊到一般地讲授新概念的方法，符合人们从感性到理性的认识事物的规律．但是，在这里我们要注意，从认识事物的原型到认识事物的本质，这是对事物认识的质的飞跃，妥善处理好这个过程，是教学成功的关键．为此，我们在教学椭圆第二定义时，作了如下安排：
１．自读推敲，引导剖析
首先让学生自读课本Ｐ．７６例３及由此引出的椭圆第二定义，自己推敲这一定义的内涵及外延，并提出以下问题供学生思考：
（１）定义中有哪些已知条件？
（２）定点、定直线、定比在椭圆定义中的名称各是什么？
（３）定比是哪两个量的比？这两个量本身是变量还是常量？定比是什么范围的值？
（４）定点、定直线、定比一定是例３给出的数量关系（Ｆ（
吗？定点坐标、定直线方程是否可为其他的形式？
对第（１）、（２）、（３）三个问题学生容易从课本中找出答案，但第（４）个问题则一石激起千层浪，学生们议论纷纷．这时，教师启而不答．
２．通过变式，提示内涵
让学生研究课本Ｐ．７９第１０题“点Ｐ与一定点Ｆ（２，０）的距离和它到一定直线x＝８的距离的比是１：２，求点Ｐ的轨迹方程，并说明轨迹是什么图形．”
学生很快根据例３求出c＝２，又由
，得a＝４，而由
，可知满足题意．从而得点Ｐ的轨迹方程为
，所以点Ｐ的轨迹是椭圆．
接着，我将上题稍加改动，让学生研究：“点Ｐ与一定点Ｆ（２，０）的距离和它到一定直线x＝８的距离的比是
，求点Ｐ的轨迹方程，并说明轨迹是什么图形．”学生沿用上题的解法，得
，由
，得
，得轨迹方程为
，有的学生由
而提出该题题设矛盾，所以无解，也有的学生列出方程组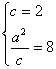
，解得
，而认为此题无解．
这时，教师不评价学生的解法，而是提示他们比较该题题意与课本给出的椭圆第二定义是否一致，由他们自己发现满足题意的动点轨迹是椭圆，进而重新寻求解题的途径．不少学生建立方程
，化简得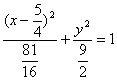
，由此可见，这是中心在点（
，对称轴为直线
及
的椭圆．
从该例让学生看到椭圆第二定义中的定点、定直线、定比的数量关系不一定是课本Ｐ．７６例３给出的定点Ｆ（c，０）、定直线
、定比
，当不满足这个数量关系时，建立椭圆方程不能套用例３的结果去解．当给出定点Ｆ（n，０）、定直线x＝m（m≠n）、定比为e（０＜e＜１时，可建立方程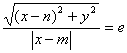
，解得
．
显然，只要m≠n，即点Ｆ（n，０）不在直线x＝m上时，都是椭圆方程．
这样，就让学生自己在解决问题的过程中，求得思考题（４）的第一个问题的答案．进而指导学生深入推敲椭圆第二定义，让他们深切地理解定义中的定点一般为(x0,y0)，定直线一般为ax＋by＋c＝０，并告诉学生在学过坐标变换之后，可通过坐标变换，将所求的轨迹方程化为椭圆的标准方程．
通过以上研究，让学生明确：课本Ｐ．７６例３题设中给出的数量关系是椭圆的标准方程的条件，而不是所有椭圆方程所要求的条件，即不是椭圆方程的本质特征，这样，学生对椭圆第二定义的内涵和外延的理解就深刻多了．
３．列举反例，防患未然
要使学生深刻理解新概念，除了要正面剖析概念，运用变式比较，揭示概念本质以外，我们还经常列举一些反例让学生判别，防止常见错误的发生．为此，给出以下两例，让学生判别命题是否正确．
例１ 点Ｐ到点Ｆ（２，０）的距离比它到定直线x=7的距离小１，点Ｐ的轨迹是什么图形？
给出如下解法让学生判别：
解：设Ｐ点的坐标为（x,y），则
而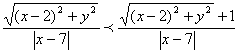
＝１，
所以点Ｐ到定点Ｆ（２，０）的距离与它到定直线x=7的距离的比小于１，故点Ｐ的轨迹是椭
圆．
例２ 点Ｐ到定直线x=8的距离与它到点Ｆ（２，０）的距离的比为
，则点Ｐ的轨迹是椭圆．
对上述两个问题，引导学生逐一分析，让学生明确：例１中，比值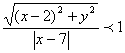
，但不是一个常数，故不可断定点Ｐ的轨迹是椭圆．例２中要注意椭圆第二定义中的定比是动点到定点的距离比动点到定点直线的距离，其比的前后项顺序不可倒置，故不可断定此题中的点Ｐ的轨迹是椭圆．经过对上述两例中典型错误的剖析，学生对椭圆第二定义的本质属性有了更深刻的认识．
４．设置新题，检测运用
经过前面的教学过程，应该说基础知识已经讲清了．但是，要让学生深刻理解教学的内容，并且能够正确运用，这需要让学生有一个独立运用所学知识解决问题的过程．于是，我们让学生独立解以下题目：一动点Ｐ到直线2x＋y－８=0的距离与它到点（１，２）的距离的比值为
，求动点Ｐ的轨迹方程，并判断点Ｐ的轨迹是何种曲线．
解：设Ｐ点的坐标为（x,y），则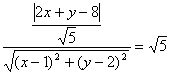
．
从方程看，现在我们还不能判定此方程的曲线是何种曲线，但仔细分析题意，可将已知条件改述为动点Ｐ到点（１，２）的距离与它到直线２x＋y－８＝０的距离之比为１：
，这显然符合椭圆第二定义，可知Ｐ点的轨迹为椭圆．
通过这一例的教学让学生更深切地理解了椭圆的第二定义，也让学生看到椭圆的非标准方程所具有的形式．
５．拓展课本，活化知识
课本对于椭圆的准线方程作了如下叙述：“对于椭圆
，相应于焦点Ｆ（c，０）的准线方程为
，根据椭圆的对称性，相应于焦点Ｆ′（－c，０）的准线方程为
；所以，椭圆有两条准线．”由此启发学生看到命题（称做Ａ）：点Ｍ（x,y）与定点Ｆ′（－c，０）的距离与它到直线l′：
的距离之比是常数
（a＞c＞０），则点Ｍ（x，y）的轨迹方程也是椭圆的标准方程．于是我们引导学生明确结论：课本Ｐ．７６例３给出的数量关系：定点Ｆ（c，０）、定直线l：
、常数
（a＞c＞０），以及命题Ａ给出的数量关系：定点Ｆ′（－c，０）、定直线l′：
、常数
（a＞c＞０）均分别是动点Ｍ的轨迹方程为椭圆标准方程的充要条件，并且，二者是等价的．接着，我们又引导学生再次分析本文第２部分所讲到的命题（称为Ｂ）：定点为Ｆ（n，０），定直线为x＝m（m≠n），定比为e（０＜e＜１ ，得出的椭圆方程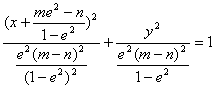
．让他们看到当且仅当
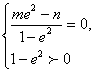即
时，动点Ｍ的轨迹方程为椭圆的标准方程．即条件“
”是动点Ｍ的轨迹方程为椭圆标准方程的充要条件．
在此基础上，要求学生自行命题，设计出动点的条件，使其轨迹方程分别符合下列要求：
①轨迹方程为椭圆的标准方程；
②轨迹方程为中心在x轴上且短轴平行于y轴的椭圆方程．
从而，让学生不但能正确地解命题Ｂ型的问题，而且能自行设计命题Ｂ型的问题，使学生对椭圆第二定义的理解、掌握和运用达到新的境界．
中考 高考名著
常用成语