四种命题（四）人教选修

教学目标：1.使学生初步掌握反证法的概念及反证法证题的基本方法．

2.培养学生用反证法简单推理的技能，从而发展学生的思维能力．

教学重点：反证法证题的步骤．

教学难点：理解反证法的推理依据及方法．

教学方法：讲练结合教学．

教具准备：多媒体．

教学过程

一、复习回顾

初中已学过反证法，什么叫做反证法？

（从命题结论的反面出发，引出矛盾，从而证明原命题成立，这样的证明方法叫做反证法.）

本节课将进一步研究反证法证题的方法.

二、讲授新课

反证法证题的步骤是什么？

（共分三步：

（1）假设命题的结论不成立，即假设结论的反面成立；

（2）从假设出发，经过推理论证，得出矛盾；

（3）由矛盾判定假设不正确，从而肯定命题的结论正确.）

反证法是一种间接证明命题的基本方法。在证明一个数学命题时，如果运用直接证明法比较困难或难以证明时，可运用反证法进行证明．反证法的基本思想：通过证明命题的否定是假命题， 从而说明原命题是真命题．

例如：“在ΔABC中，若∠C是直角，那么∠B一定是锐角．”显然命题的结论是正确的，但直接证明是较困难的，而用反证法就容易证明之．请一同学证明．

（注意 ：因∠B不是锐角有两种情况，即∠B为直角或钝角，必须对两种可能均加以否定，才能证明∠B一定是锐角．）

由此在运用反证法证明命题中如果命题结论的反面不止一个时，必须将结论所有反面的情况逐一驳证，才能肯定原命题的结论正确．

下面看例题：

例1：用反证法证明：如果a>b>0,那么

说明：假设不大于，即或．

∵ a>0,b>0，;∴与

即， ∴ (推理利用了不等式的传递性)．

又由 ∴，但这些都与已知条件矛盾．

∴成立．

例2：用反证法证明：圆的两条不是直径的相交弦不能互相平分．

已知：如图：在⊙0中，弦AB、CD交于点p，且AB、CD不是直径．

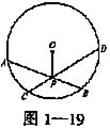求证：弦AB、CD不被p平分．

证明：假设弦AB、CD被p平分，连结Op，由平面几何知识可推出：

Op⊥AB且Op⊥CD

又推出：在平面内过一点p有两条直线

AB和CD同时与Op垂直，这与垂线性质矛盾，则原命题成立．

由上述两例题可看：利用反证法证明时，关键是从假设结论的反面出发，经过推理论证，得出相矛盾的结论，这是由假设所引起的，因此这个假设是不正确的，从而肯定了命题结论的正确性．

反证法证题的关键是：第二步即从结论的反面出发，经过推理论证，得出矛盾．反证法引出的矛盾有以下几种情况：

（1）与原题中的条件矛盾；

（2）与定义、公理、定理、公式等矛盾；

（3）与假设矛盾．

例3：若p>0,q>0,p³＋p³=2.试用反证法证明：p＋q≤2．

分析：此题直接由条件推证p＋q≤2是较难的，由此用反证法证之．

证明：假设p＋q>2,

∵p>0,q>0.

（p＋q）³=p³＋3p²q＋3pq²＋q³>8.

又∵p³＋q³=2。

∴代入上式得：3pq(p＋q)>6,即：(pq(p＋q)>2.……(1)

又由p³＋q³=2，即(p＋q)(p²-pq＋q²)=2代入（1）得：

pq(p＋q)>(p＋q)(p²-pq＋q²).

但这与（p-q）²≥0矛盾，∴假设p＋q>2不成立．

故p＋q≤2.

反证法是一种证明题目的间接方法，在有些题目的证明中用反证法非常简洁，但并不是每一题用反证都恰倒好处，那么，对于哪些题目适合用反证法呢？

从这些条件推出所知的也很少或无法用已知条件进行直接证明的．

当问题中能用来作为推理依据的公理、定理很少，无法直接证明或证明无从下手的．

结论以否定的形式出现，无法引用定理来证明否定形式的结论．

对要证明的命题，已知它的逆命题是正确的．

要求证明的命题适合某种条件的结论唯一存在．

对反证法的掌握，还有待于随着学习的深入，逐步提高．

例4．用反证法证明：是无理数

证明：假设不是无理数，即是有理数

则设=（是互质的正整数）

则，

，

是偶数，

设（是正整数），

则即，

为偶数 则都是偶数，此与互质矛盾．

因此，假设“不是无理数”不正确．

所以，是无理数．

三、课堂练习：课本p33 1、2

四、课堂小结

本节重点研究了反证法证题的一般步骤及反证法证明命题的应用．

对于反证法的熟练掌握还需在今后随着学习的深入，逐步加强和提高．

五、课后作业

书面作业：课本p34，习题1.7中第5题．

预习：下节内容，预习提纲：

1.充分条件与必要条件的意义是什么？

2.命题“若p则q”的真假与p是q的充分条件，q是p的必要条件的关系是什么？

六、板书设计 §1.7.3 反证法

1.反证法证明命题的步骤．

2.反证法应用：例题．

小结：

七、教学后记：