两角和与差的正弦、余弦、正切的综合练习⑶ 人教必修
目的:进一步熟悉有关技巧,继续提高学生综合应用能力。(采用《精编》例题)
过程:一、求值问题(续)
例一 若tana=3x,tanb=3-x, 且a-b=![]() ,求x的值。
,求x的值。
解:tan(a-b)=tan![]() =
=![]() ∵tana=3x,tanb=3-x
∵tana=3x,tanb=3-x
∴![]()
∴3 3x-3 3-x=2![]() 即:
即:![]()
∴![]() (舍去) ∴
(舍去) ∴![]()
例二 已知锐角a, b, g 满足sina+sing=sinb, cosa-cosg=cosb, 求a-b的值。
解:∵sina+sing=sinb ∴sina -sinb = -sing<0 ①
∴sina 同理:∵cosa-cosg=cosb ∴ cosa- cosb = cosg ② ①2+②2: 1+1-2cos(a-b)=1 ∴cos(a-b)= ∵ 二、关于最值问题 例三 已知tana,tanb是关于x的方程 解:∵tana,tanb是方程 ∴△=4(7m-3)-8m2≥0 ∴2m2-7m+3≤0 解之: 又: 为求范围: ∵ ∴当 当 ∴ ∴p-q+1=0 例四 若 解:f(x)= ∵ ∴ 即: 当且仅当 例五 已知f(x)=-acos2x- 解:f(x)=-acos2x- =-2asin(2x+ ∵x [0, 又: a>0 ∴-2a<0 ∴ ∴ ∵-5≤f(x)≤1 ∴ ∴g(t)=at2+bt-3=2t2-5t-3=2(t- ∴当t=0时,g(t)min=g(0)=-3 三、作业:《精编》 p61 6、7、11 p62 20、22、23、25![]()
![]()
![]() ∴
∴![]() ∴a-b=
∴a-b=![]()
![]() 的两个实根,求tan(a+b)的取值范围。
的两个实根,求tan(a+b)的取值范围。![]() 的两个实根
的两个实根![]() ≤m≤3
≤m≤3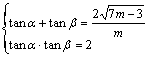 ∴
∴![]()
![]()
![]() ≤m≤3 ∴
≤m≤3 ∴![]() ≤m≤2
≤m≤2![]() 时,
时,![]() 有最大值
有最大值![]()
![]() 或
或![]() 时,
时,![]() 有最小值2
有最小值2![]() 即:
即:![]()
![]() ,求f(x)=
,求f(x)=![]() sinx+cosx的最大值和最小值,并求出此时的x值。
sinx+cosx的最大值和最小值,并求出此时的x值。![]() sinx+cosx=2
sinx+cosx=2![]()
![]() ∴
∴![]()
![]()
![]()
![]() 当且仅当
当且仅当![]() ,
,![]() 时f(x)min=
时f(x)min=![]()
![]() ,
,![]() 时f(x)max=2
时f(x)max=2![]() asin2x+2a+b,其中a>0,x∈[0,
asin2x+2a+b,其中a>0,x∈[0,![]() ]时,-5≤f(x)≤1,设g(t)=at2+bt-3,t [-1,0],求g(t)的最小值。
]时,-5≤f(x)≤1,设g(t)=at2+bt-3,t [-1,0],求g(t)的最小值。![]() asin2x+2a+b=-2a[
asin2x+2a+b=-2a[![]() sin2x+
sin2x+![]() cos2x]+2a+b
cos2x]+2a+b![]() )+2a+b
)+2a+b![]() ] ∴
] ∴![]() ∴
∴![]()
![]()
![]() ∴
∴![]()
![]()
![]() )2-
)2-![]() ∵t [-1,0]
∵t [-1,0]
中考 高考名著
常用成语