两角和与差的三角函数 人教必修6
教学目标
(一)知识目标
两角和与差的余弦、正弦、正切公式.
(二)能力目标
进一步熟练掌握两角和与差的余弦、正弦、正切公式的灵活应用.
(三)德育目标
1.提高学生的推理能力；
2.培养学生用联系变化的观点看问题；
3.提高学生的数学素质；
4.使学生树立科学的世界观.
教学重点
利用两角和与差的余弦、正弦、正切公式解决一些综合性问题.
教学难点
怎样使学生对所学知识融会贯通，运用自如.
教学方法
通过强化练习，掌握各个公式的结构特征，以达到灵活应用.(自学辅导法)
教具准备
投影片一张（§4.6.7 A）
练习题
1.若方程x2＋ｍx＋ｍ＋1＝0的两根为tanα、tanβ.求证sin(α＋β)＝cos（α＋β）
2.若△ABC的三内角成等差数列，且A＜B＜C，tanAtanC＝2＋
，求角A、B、C的大小.
3.如果sinα＋sinβ＝a，cosα＋cosβ＝b，ab≠0，则cos（α－β）等于 ( )
A.
B.
C.
Ｄ.
教学过程
Ⅰ.复习回顾
师：再来回顾一次和、差角公式.
生：cos（α±β）＝cosαcos&betasinαsinβ
sin（α±β）＝sinαcosβ±cosαsinβ
tan（α±β）＝
Ⅱ.讲授新课
［例1］已知一元二次方程ax2＋bx＋c＝0(a≠0且a≠c)的两个根为tanα、tanβ，求tan（α＋β）的值.
分析:由题意可得tanα、tanβ为一元二次方程的两根,由韦达定理可知tanα＋tanβ＝－
，且tanα·tanβ＝
，联想两角和的正切公式，不难求得tan（α＋β）的值.
解：由a≠0和一元二次方程根与系数的关系，可知：
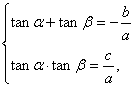且a≠c
所以tan（α＋β）＝
评述：在解题时要先仔细分析题意，联想相应知识，选定思路，再着手解题.
［例2］设sinθ＋cosθ＝
，
＜θ＜π，求sin3θ＋cos3θ与tanθ－cotθ的值.
解：∵sinθ＋cosθ＝
∴sin2θ＋2sinθcosθ＋cos2θ＝
∴sinθcosθ＝－
又sin3θ＋cos3θ＝（sinθ＋cosθ）（sin2θ－sinθcosθ＋cos2θ）
＝（sinθ＋cosθ）（1－sinθcosθ）
＝
（1＋
）＝
又∵
＜θ＜π
∴sinθ＞0，cosθ＜0
∴sinθ－cosθ＝
∴tanθ－cotθ＝
评述：（1）在sinθ＋cosθ、sinθcosθ与sinθ－cosθ中，知其中之一便可求出另外两个.
（2）解决有关sinθ＋cosθ、sinθcosθ与sinθ－cosθ的问题是三角函数中的一类重要问题.
Ⅲ.课堂练习
(打出投影片§4.6.7 A，让学生练习)
生：1解：由题意可知
由：
得：tan（α＋β）＝
即：sin（α＋β）＝cos（α＋β）
∴命题得证.
师：评述：要注意已知条件与所求结论中涉及三角函数的关系，选择适当的关系式进行转化.
师：2分析：由A、B、C为△ABC的三内角，可知A＋B＋C＝180°，又已知A、B、C为等差数列，即2B＝A＋C，所以B＝60°且A＋C＝120°与已知条件中的tanAtanC＝2＋
可联系求出tanA、tanC，从而确定A、C.
生：解：由题意知：
解之得：B＝60°且A＋C＝120°
∴tan（A＋C）＝tan120°＝－
＝
又∵tanAtanC＝2＋
∴tanA＋tanC＝tan（A＋C）（1－tanAtanC）＝tan120°(1－2－
）
＝－
（－1－
）＝3＋
∵tanA、tanC可作为一元二次方程
x2－（3＋
）x＋（2＋
）＝0的两根
又∵0＜A＜B＜C＜π
∴tanA＝1 tanC＝2＋
即：A＝45°，C＝75°
答：A、B、C的大小分别为45°、60°、75°.
师：评述：要注意挖掘隐含条件，联想相关知识，构造方程等等.
师：3.分析:由已知条件中的两关系式结合同角三角函数的平方关系式sin2α＋cos2α＝1不难求得cos（α－β），再利用平方关系求得sin（α－β）.
生：解：由
得：a2＋b2＝sin2α＋sin2β＋2sinαsinβ＋cos2α＋cos2β＋2cosαcosβ
＝2＋2cos（α－β）
∴cos（α－β）＝
－1
师：评述：遇到这种已知条件式时，往往要结合同角三角函数平方关系式.
Ⅳ.课时小结
在解决三角函数问题时，常常要将和角公式、差角公式、诱导公式、同角三角函数基本关系式等等综合使用.
Ⅴ.课后作业
(一)课本p419 、10 p4214
(二)1.预习课本p42～p43.
2.预习提纲：
（1）如何利用和角公式推导倍角公式
（2）和角公式与倍角公式的关系如何
（3）为什么把倍角公式化归到和角公式的范畴
板书设计
课题 | ||
课时小结 | 例题 | 复习回顾 |
备课资料
1.tan2A·tan（30°－A）＋tan2Atan（60°－A）＋tan（30°－A）tan（60°－A）＝.
解：原式＝tan2A［tan（30°－A）＋tan（60°－A）］＋［tan(30°－A)tan（60°－A）］
＝tan2Atan［（30°－A）＋（60°－A）］［1－tan（30°－A）tan（60°－A）］＋
［tan（30°－A）tan（60°－A）］
＝tan2Atan（90°－2A）［1－tan（30°－A）tan（60°－A）］＋［tan（30°－A）
tan（60°－A）］
＝tan2A·cot2A［1－tan(30°－A）tan(60°－A）］＋［tan(30°－A）tan（60°－A）］＝1
师：评述：先仔细观察式子中所出现的角，灵活应用公式进行变形，然后化简、求值.
2.已知tanα、tanβ是方程x2－3x－3＝0的两个根,求sin2（α＋β）－3sin（α＋β）cos（α＋β）－3cos2（α＋β）的值.
解：由题意知
∴
sin2（α＋β）－3sin（α＋β）cos（α＋β）－3cos2（α＋β）
＝cos2（α＋β）［tan2（α＋β）－3tan（α＋β）－3］
＝
［tan2（α＋β）－3tan（α＋β）－3］
＝
3.已知α、β为锐角，cosα＝
，tan（α－β）＝－
，求Cosβ的值.
解：由α为锐角，cosα＝
，∴sinα＝
.
由α、β为锐角，又tan（α－β）＝－
∴cos（α－β）＝
sin（α－β）＝－
∴cosβ＝cos［α－（α－β）］＝cosα·cos（α－β）＋sinα·sin（α－β）
＝
教学后记
中考 高考名著
常用成语