两角和与差的三角函数 人教必修2
教学目标
(一)知识目标
1.两角和的正切公式；
2.两角差的正切公式.
(二)能力目标
1.掌握T（α＋β），T（α－β)的推导及特征；
2.能用它们进行有关求值、化简.
(三)德育目标
1.提高学生简单的推理能力；
2.培养学生的应用意识；
3.提高学生的数学素质.
教学重点
两角和与差的正切公式的推导及特征.
教学难点
灵活应用公式进行化简、求值.
教学方法
结合典型习题使学生掌握公式的各种变形，以致于灵活应用公式.(自学辅导法)
教具准备
幻灯片一张（§4.6.4 A）
练习题
1.化简下列各式
(1)tan（α＋β）·（1－tanαtanβ）
(2)
(3)
2.求值：
(1)
(2)
(3)tan21°(1＋tan24°）＋tan24°
教学过程
Ⅰ.复习回顾
师：首先，我们来回顾一下前面所推导两角和与差的余弦、正弦公式.
(学生作答，老师板书)
sin（α＋β）＝sinαcosβ＋cosαsinβ（Ｓ（α＋β））
sin（α－β）＝sinαcosβ－cosαsinβ（Ｓ（α－β））
cos（α＋β）＝cosαcosβ-sinαsinβ（C（α＋β））
cos（α－β）＝cosαcosβ＋sinαsinβ（C(α-β））
师：要准确把握上述各公式的结构特征.
Ⅱ.讲授新课
一、推导公式
师：上述公式结合同角三角函数的基本关系式，我们不难得出：当cos（α＋β）≠0时tan（α＋β）＝
如果cosαcosβ≠0，即cosα≠0且cosβ≠0，我们可以将分子、分母都除以
cosαcosβ，从而得到：
tan（α＋β）＝
不难发现，这一式子描述了两角α与β的和的正切与这两角的正切的关系.
同理可得：tan（α－β）＝
或将上式中的β用－β代替，也可得到此式.
这一式子又描述了两角α与β的差的正切与这两角的正切的关系.
所以，我们将这两式分别称为两角和的正切公式、两角差的正切公式，简记为T（α＋β），T（α－β）.
但要注意：运用公式T（α±β）时必须限定α、β、α±β都不等于
＋kπ（k∈Ｚ）.
因为tan（
＋kπ）不存在.
师：下面我们看一下它们的应用
二、例题讲解
［例1］不查表求tan75°，tan15°的值.
解：tan75°＝tan（45°＋30°）＝
tan15°＝tan（45°－30°）＝
［例2］求下列各式的值
（1）
（2）
(1)分析：观察题目结构，联想学过的公式，不难看出可用两角差的正切公式.
解：
(2)分析：虽不可直接使用两角和的正切公式，但经过变形可使用之求解.
解：由tan150°＝tan（75°＋75°）＝
得：
说明：要熟练掌握公式的结构特征，以灵活应用.
［例3］利用和角公式计算
的值.
分析：因为tan45°＝1，所以原式可看成
这样，我们可以运用正切的和角公式，把原式化为tan（45°＋15°），从而求得原式的值.
解：∵tan45°＝1
∴
说明：在解三角函数题目时，要注意“1”的妙用.
Ⅲ.课堂练习
(打出幻灯片§4.6.4 A，学生练习)
生：解：1.（1）tan（α＋β）（1－tanαtanβ）＝
（1－tanαtanβ）
＝tanα＋tanβ
(2)
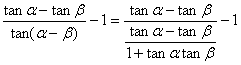＝1＋tanαtanβ－1＝tanαtanβ
(3)
＝tan［（α－β）＋β］＝tanα
说明：这一题目若将tan（α－β）用两角差的正切公式展开，则误入歧途，要注意整体思想.
2.解：(1)
(2)
(3)分析：因为tan21°＝tan（45°－24°）＝
又因为tan45°＝1
所以，1＋tan24°＝1＋tan45°tan24°
这样，可将原式化为：tan（45°－24°）（1＋tan45°tan24°）＋tan24°
从而求得原式的值.
解：tan21°（1＋tan24°）＋tan24°＝tan（45°－24°）（1＋tan45°tan24°）＋tan24°
＝
（1＋tan45°tan24°）＋tan24°＝1
Ⅳ.课时小结
正切的和、差角公式以及它们的等价变形.
这些公式在化简、求值、证明三角恒等式时都有不少用处.
Ⅴ.课后作业
(一)课本p41习题4.6 4，6
(二)1.预习课本p39.
2.总结两角和差公式的推导体系.
板书设计
课题 | |
公式及推导 | 例题 |
备课资料
1.已知
，且θ∈（π，
），则tan（θ－
）的值为多少
解：∵cosθ＝－
且θ∈（π，
）
∴sinθ＝－
则tanθ＝
∴
2.若tan（α＋β）＝
，tan（β－
）＝
，求tan（α＋
）的值.
分析：注意已知角与所求角的关系，则可发现（α＋
）＋（β－
）＝α＋β，所以可将α＋
化为（α＋β）－（β－
），从而求得tan（α＋
）的值.
解：tan（α＋
）＝tan［（α＋β）－（β－
)］
＝
将tan（α＋β）＝
，tan（β－
）＝
代入上式则，原式＝
3.已知tanα＝
，tan（α－β）＝－
，求tan（β－2α)
解：∵α＋（α－β）＝2α－β
∴tan（β－2α）＝tan［－（2α－β）］＝－tan（2α－β）＝－tan［α＋（α－β)］
＝
4.证明
分析：细心观察已知等式中的角，发现它们有隐含关系：
，
∴
①
②
①÷②即得：
.
教学后记
中考 高考名著
常用成语