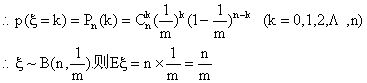离散型随机变量的分布列(3) 人教选修
课 题:第3课 离散型随机变量的期望与方差(1)
课 型:新授课
课时计划:本课题共安排1课时
教学目的:
1.了解离散型随机变量的期望的意义,会根据离散型随机变量的分布列求出期望。
2.理解公式“E(aξ+b)=aEξ+b”,以及“若ξ~B(n,p),则Eξ=np”。能熟练地应用它们求相应的离散型随机变量的期望。
教学重点、难点:离散型随机变量的期望的意义;会求相应的离散型随机变量的期望
教具使用:常规教学
教学过程:
1.复旧引新
(1)离散型随机变量的分布列的概念、性质.
(2)离散型随机变量服从二项分布的概念、例子.
(3)提出教科书中“某射手射击所得环数ξ的分布列”的例子,可问:我们能否通过计算,预计该射手n次射击的平均环数
2.提出离散型随机变量ξ的数学期望Eξ的概念及公式E(aξ+b)=aEξ+b
在复习、思考、计算与讨论的基础上,教师可问:从多名射手中选拔一名参加射击比赛,我们能否根据他们各自射击的平均成绩(数学期望)作为选拔的一项标准同时概括出:
一般地,若离散型随机变量ξ的概率分布为
| ξ | x1 | x2 | … | xn | … |
p | p1 | p2 | … | pn | … |
则称Eξ= x1 p1 + x2 p2 +…+ xn pn +…为ξ的数学期望或平均数、均值.数学期望简称为期望。
根据数学期望的概念及前面所学知识,推导出公式
| E(aξ+b)= aEξ+b |
3.讲解例1、例2
例1 解答本章引言中的一个问题,这家商场应该采取哪种促销方式
估计学生对教科书中的例1和例2的理解不存在困难,所以讲此例之前可布置学生自学这两道例题。
例2 接第1课例3,若随机变量的概率分布为
| ξ | 15 | 16 | 17 | 18 |
p | 0.1 | 0.5 | 0.3 | 0.1 |
求所收租车费η的数学期望.
| 解:依题意,得 Eη=15╳0.1+16╳0.5+17╳0.3+18╳0.1=16.4
答:所收租车费V的期望是34.8元. |
4.讲解例3(即教科书中例3)
5.提出并推导
| 若ξ~B(n,p),则Eξ=np |
推导公式后,布置学生自学教科书中的例4。
6.讲解例4
例4 设有m升水,其中含有n个大肠杆菌,今任取1升水检验,设其中含大肠杆菌的个数为ξ,求Eξ。
分析:任取1升水,此升水中含一个大肠杆菌的概率是1/m,事件“ξ=k”发生,即n个大肠杆菌中恰有k个在此升水中。由n次独立重复试验中事件A(在此升水中含一个大肠杆菌)恰好发生k次的概率计算方法可求出p(ξ=k ),进而可Eξ。
| 解:记事件A:“在所取1升水中含一个大肠杆菌”,则p(A)=1/m
|
7.课堂练习
做教科书第12页中的“练习” 。
8.归纳总结
(1)本课从一个具体例子人手,引入离散型随机变量的期望的概念和意义,介绍了公式E(aξ+b)= aEξ+b,以及服从二项分布的随机变量的期望Eξ=np。
(2)对学生做的练习进行点评。
布置作业:
教科书习题1.2第1、4、5、6题
教学反馈
板书设计
中考 高考名著
常用成语