空间向量及其加减与数乘运算 人教选修

空间向量及其加减与数乘运算

教学目标：理解空间向量的概念，掌握空间向量的加法、减法和数乘运算。

教学重点：理解空间向量的概念，掌握空间向量的加法、减法和数乘运算。

教学过程：

一、复习：

1、平面向量的概念

2、平面向量的加减和数乘运算

二、授新课：

1．空间向量的概念

在空间，我们把具有大小和方向的量叫做向量。

注：⑴空间的平移就是一个向量。

⑵向量一般用有向线段表示。同向等长的有向线段表示同一或相等的向量。

⑶空间的两个向量可用同一平面内的两条有向线段来表示。

2．空间向量的运算

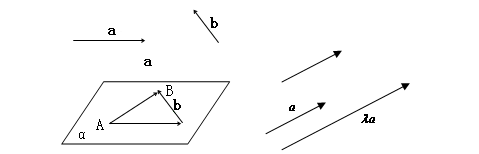
定义：与平面向量运算一样，空间向量的加法、减法与数乘向量运算如下（如图）

运算律：⑴加法交换律：

⑵加法结合律：

⑶数乘分配律：

3．平行六面体：

平行四边形ABCD平移向量a到的轨迹所形成的几何体，叫做平行六面体，并记作：ABCD－。它的六个面都是平行四边形，每个面的边叫做平行六面体的棱。

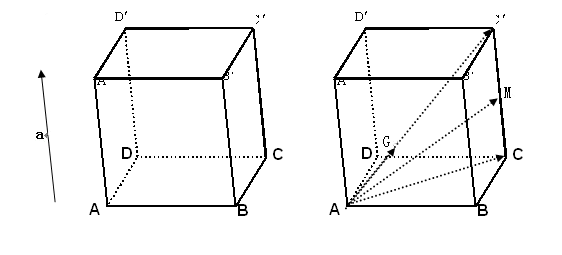
4．举例：

例1、已知平行六面体ABCD－化简下列向量表达式，标出化简结果的向量：

⑴； ⑵；

⑶； ⑷。

解：如图：

⑴； ⑵=；

⑶设M是线段的中点，则；

⑷设G是线段的三等份点，则。

向量如图所示。

三、做练习：第27页第1、2题

四、小结：1、空间向量的概念

2、空间向量的运算

3、平行六面体的概念

五、布置作业：

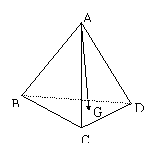
如图设A是△BCD所在平面外的一点，G是△BCD的重心。求证：