函数的最大最小值 人教选修

教学目标：1、使学生掌握可导函数在闭区间上所有点（包括端点）处的函数中的最大（或最小）值；

2、使学生掌握用导数求函数的极值及最值的方法

教学重点：掌握用导数求函数的极值及最值的方法

教学难点：提高“用导数求函数的极值及最值”的应用能力

一、复习：

1、；2、

3、求y=x³—27x的 极值。

二、新课

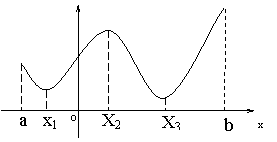在某些问题中，往往关心的是函数在一个定义区间上，哪个值最大，哪个值最小

观察下面一个定义在区间上的函数的图象

发现图中____________是极小值，_________是极大值，在区间上的函数

的最大值是______，最小值是_______

在区间上求函数的最大值与最小值 的步骤：

1、函数在内有导数 ；

2、求函数在内的极值

3、将函数在内的极值与比较，其中最大的一个为最大值 ，最小的一个为最小值

三、例1、求函数在区间上的最大值与最小值。

解：先求导数，得

令＝0即解得

导数的正负以及，如下表

从上表知，当时，函数有最大值13，当时，函数有最小值4

在日常生活中，常常会遇到什么条件下可以使材料最省，时间最少，效率最高等问题，这往往可以归结为求函数的最大值或最小值问题。

例2用边长为60CM的正方形铁皮做一个无盖的水箱，先在四个角分别截去一个小正方形，然后把四边翻转90°角，再焊接而成，问水箱底边的长取多少时，水箱容积最大，最大容积是多少？

例3、已知某商品生产成本C与产量p的函数关系为C＝100＋4p，价格R与产量p的函数关系为R＝25－0.125p，求产量p为何值时，利润L最大。

四、小结：

1、闭区间上的连续函数一定有最值；开区间内的可导函数

不一定有最值，若有唯一的极值，则此极值必是函数的最值。

2、函数在其定义区间上的最大值、最小值最多各有一个，而函数的极值可能不止一个，也可能没有一个。

3、在解决实际应用问题中，关键在于建立数学模型和目标函数；如果函数在区间内只有一个极值点，那么根据实际意义判断是最大值还是最小值即可，不必再与端点的函数值进行比较。

五、练习及作业：：

1、函数在区间上的最大值与最小值

2、求函数在区间上的最大值与最小值。

3、求函数在区间上的最大值与最小值。

4、求函数在区间上的最大值与最小值。

5、给出下面四个命题

（1）函数在区间上的最大值为10，最小值为－

（2）函数（2＜X＜4）上的最大值为17，最小值为1

（3）函数（－3＜X＜3）上的最大值为16　，　最小值为－16

（4）函数（－2＜X＜2）上　无　最大值　也无　最小值。

其中正确的命题有＿＿＿＿＿＿＿＿＿＿＿＿

6、把长度为L CM的线段分成四段，围成一个矩形，问怎样分法，所围成矩形的面积最大。

7、把长度为L CM的线段分成二段，围成一个正方形，问怎样分法，所围成正方形的面积最小。

8、某商品一件的成本为30元，在某段时间内，若以每件X元出售，可以卖出(200-X)件，应该如何定价才能使利润L最大？