函数的单调性 教学设计 人教必修2

教学目标

1．教学内容：函数单调性的应用及函数单调区间的求法

2．教学目的要求

(1) 深化函数单调性的概念，掌握函数单调区间的求法．

(2) 会利用函数单调性解决比大小、求值域、求最值等问题，会判断复合函数的单调性．

(3) 通过函数单调性有关知识的纵横延伸，培养学生思维的发散性．

设计思想

深化函数单调性的概念，加深对函数单调性重要性的认识，理解和掌握函数单调性的各种应用，在理解概念的基础上，通过一些典型例题拓宽和加深对有关知识的认识，引导学生多渠道、多角度去思考，在更深、更广的领域内挖掘知识的内在联系，探求问题的纵横延伸，在实施转化的过程中培养学生思维品质．

1．明确函数的单调区间的求法

2．介绍复合函数的意义，给出判断复合函数的单调性和求单调区间的方法和步骤

3．说明函数单调性的各种应用

教学过程

一、课题引入

1．复习函数单调性的概念，并说明根据单调性定义证明和判断函数单调性的步骤

2．求一些简单函数的单调区间

3．总结函数单调区间的求法

二、知识讲解

1．函数的单调区间的求法

(1) 图像法；(2)定义法；(3)利用已知函数的单调性．

2．复合函数的意义(严格定义请参看上节课“函数单调性(一)”的“引伸和提高”部分)．另外可以给学生介绍下面的描述

如果y是u的函数，而u是x的函数，即y=f(u)，u=g(x)，那么y关于x的函数y=f[g(x)]叫做函数f和g的复合函数，u为中间变量．

3．复合函数单调性的规律：内外层函数同增同减则增，一增一减则减．

4．函数单调性的应用

(1) 利用函数的单调性比较大小．

(2) 确定函数的值域或求函数的最值．

(3) 利用函数的单调性解或证不等式．

(4) 利用函数的单调性解方程．

(5) 利用函数的单调性简化画函数图像的过程．

三、例题分析

例6．判断函数在(1，＋∞)上的单调性．

解：．

当x>1时，u=(x＋2)²－4是增函数．

则在(1，＋∞)是减函数．

∴ 原函数在区间(1，＋∞)上是减函数．

点评：将函数变形，转化成一些基本初等函数，利用基本函数的单调性讨论较复杂函数的单调性．

例7．已知二次函数f(x)=x²＋bx＋c，对任意x∈R，都有f(1＋x)=f(1－x)，试比较与f(－a²＋a－1) (a∈R)的大小

解：由f(1＋x)=f(1－x)知函数f(x)=x²＋bx＋c的图像关于直线x=1对称．∴当x∈时，f(x)是单调递减的．

又

∴f(－a²＋a－1)≥

而

∴f(－a²＋a－1)≥

点评：利用函数的单调性比较两个函数值的大小，要注意自变量取值要在同一个单调区间内．本题就是利用二次函数图像的对称性把转换到，这样与－a²＋a－1就在f(x)的同一单调区间内．

例8．若x，y∈R，且满足3x²＋2y²=6x，求x、y取何值时，x²＋y²取得最大值，并求出这个最大值．

解：由已知得，解得，0≤x≤2．

其中x∈[0，2]．此函数图像的对称轴方程为x=3．当x∈[0，2]时，函数是递增的．

∴ 当x=2时，x²＋y²取得最大值，最大值为4．

点评：利用函数的单调性求最值，注意x的取值范围即定义域和增减区间．

例9．求函数的值域．

解：令，t≥0

则

∴

(t≥0)

∴ 当t=1时．ymax=1，当t∞时，y－∞

∴

四、习　题

1．函数y=f(x)是定义域R上的减函数，则函数f(|x＋2|)的单调减区间是()

(A)R (B) (－∞，－2) (C) (－2，＋∞) (D) (－∞，2)

2．函数的值域是_________________________

3．函数y=2x²＋8x－1，x∈[－3，1]，则其最小值为_________，最大值为__________．

答　案

1．C 2．3．－9，9．

五、小结或总结

1. 复合函数单调性的判断 2. 单调区间的求法 3. 比较大小 4. 函数单调性的应用求函数的最值

5. 函数的值域

六、思　考　题

1．已知函数f(x)是定义在(0，＋∞)上增函数，f(x)>0，f(2)=1．求函数(x>0)的单调区间．

2．已知函数f(x)=x²－2x＋2，x∈[t，t＋1] (t∈R)，f(x)的最小值是t的函数，记作g(t)，求g(t)的解析式．

3．求函数的最小值．

答　案1．单减区间，单增区间．

2．

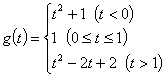
3．．