复数的向量表示 教学设计 人教选修1

教学目的

1掌握复数的向量表示 ，复数模的概念及求法，复数模的几何意义．

2 通过数形结合研究复数．

3培养学生辩证唯物主义思想．

重点难点

复数向量的表示及复数模的概念．

教学学具

投影仪

教学过程

1复习提问：向量的概念；模；复平面．

2新课：

一、复数的向量表示：

在复平面内以原点为起点，点Z（a，b）为终点的向量OZ，由点Z（a，b）唯一确定．

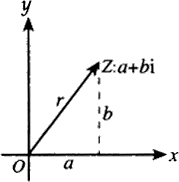
因此复平面内的点集与复数集C之间存在一一对应关系，而复平面内的点集与以原点为起点的向量一一对应．

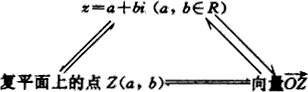
常把复数z=a＋bi说成点Z（a，b）或说成向量OZ，并规定相等向量表示同一复数．

二、复数的模

向量OZ的模（即有向线段OZ的长度）叫做复数z=a＋bi的模（或绝对值）记作|Z|或|a＋bi|

|Z|=|a＋bi|=a＋b

例1 求复数z₁=3＋4i及z_２=-1＋2i的模，并比较它们的大小．

解：∵|Z₁|²=3²＋4²=25 |Z_２|²=（-1）²＋2²=5

∴|Z₁|＞|Z_２|

练习： 1已知z₁=1＋3i z_２=-2i Z=4 Z_４=-1＋2i

⑴在复平面内，描出表示这些向量的点，画出向量．

⑵计算它们的模．

三、复数模的几何意义

复数Z=a＋bi，当b=0时z∈R |Z|=|a|即a在实数意义上的绝对值复数模可看作点Z（a，b）到原点的距离．

例2 设Z∈C满足下列条件的点Z的集合是什么图形？

⑴ |Z|=4 ⑵ 2≤|Z|＜4

解：（略）

练习：⑴ 模等于4的虚数在复平面内的点集．

⑵ 比较复数z₁=－5＋12i z_２=―6―6i的模的大小．

⑶已知：|Z|=|x＋yi|=1 求表示复数x＋yi的点的轨迹．

教学后记：

板书设计：

一、复数的向量表示： 三、复数模的几何意义

二、复数的模 例2

例1