从椭圆的标准方程推导中所发现到的 人教选修2

在“椭圆的标准方程”一节中，教材提供了椭圆的定义、椭圆的标准方程及其推导.其中，坐标系的建立、方程的化简，为我们今后学习双曲线、抛物线及一些轨迹方程的探求提供了借鉴.

当然，如果我们对椭圆标准方程的推导细细观察，会发现一个令人振奋的结论：椭圆上的点到焦点的距离公式——焦半径公式！

为行文方便，这里抄录部分教材中的推导过程.

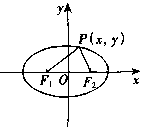如图，坐标系的建立与教材相同，设p（x,y）是椭圆C上任意一点.根据椭圆的定义：

p点到两定点F₁、F₂（|F₁F₂|=2c）距离之和是常数(2a)(a＞c)， 因此|pF₁|＋|pF₂|=2a，

即

移项，得

两边平方，整理，得4a

注意到|pF1|=所以，有|pF1|=

这样，我们就非常轻松地得到了椭圆的焦半径公式，解决了令人困惑的问题：椭圆上哪个点距焦点最近，哪个点距焦点最远，从而使有关例题、练习题、习题的解决有了理论上的根据，也改变了“没有学习椭圆的第二定义，不知焦半径公式”的被动局面.