统计调查 (第二课时)教学设计

§10.1统计调查 (第二课时)

【教学重点与难点】

教学重点：了解简单随机抽样调查的方法．

教学难点：简单随机抽样的应用．

【教学目标】

1．了解简单随机抽样的基本步骤和方法．

2.．通过抽样调查，初步感受抽样的必要性，通过案例了解简单随机抽样．

【教学方法】

通过经历对具体案例的探究了解抽样调查，体会进行抽样调查的必要性．

【教学过程】

一、创设情境 提出问题

（设计说明：在现实生活中发现并提出简单的问题，吸引学生的注意力，激发学生自主学习的兴趣和积极性．）

问题：某校有2000名学生，想要了解全校学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况，怎样进行调查?

学生只要回答合理即可．

（教学说明：这里所提出问题与第一节相响应，只是在人数上加以变化，从而引发学生的思考．）

二、探索新知 解决问题

自主探究抽样调查

（设计说明：由相同的问题引出不同的调查方法．）

问题1：第一节课探索的问题与本节课所探索的问题有什么不同?

学生回答：人数不同．第一节课只调查50名同学的情况，而本节课要调查2000名学生的情况．

教师讲解：对于这2000名学生，我们可以一一进行调查，但这么做不仅要花费很长的时间，同时也要消耗大量的人力与物力．因此，面对这种情况，我们就需要寻找一既省时省力又能解决问题的方法，这就是抽样调查．

所谓的抽样调查，是一种抽取一部分对象进行调查，然后根据调查数据推断全体对象情况的一种较为简便的方法．其中，我们要考察的全体对象称为总体，组成总体的每一个对象称为个体，被抽取的那些个体组成了一个样本．

问题2：你能说出上面问题中的总体、个体和样本都是什么吗?

学生回答：总体是全校学生，个体是学校里的每一个学生，而抽取出来的所有学生组成了一个样本．

问题3：你认为抽取多少名学生进行调查比较合适?

学生回答的人数适量即可．

问题4：我们所抽取的学生的人数就叫做样本容量，即样本中个体的数量．你认为在抽取样本的时候应注意哪些问题?

学生讨论回答：抽取的样本应具有代表性和广泛性．

问题5：你有什么方法可以使每位同学被抽到的机会相等．

学生只要回答得合理即可．

教师讲解：下面是某同学抽取样本容量为100的调查数据统计表．像这样总体中的每一个个体都有相等的机会被抽到，这样的抽样方法就叫简单随机抽样．

抽样调查100名学生最喜爱节目的人数统计表

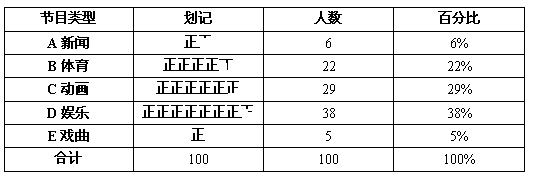表格中的数据也可以用条形图和扇形图来描述（如下图），

从这几个图表中，你能得到哪些信息?

学生回答：可以根据已有的数据估算出全校学生喜欢各类节目所占的百分比等．

问题7：你能举出生活中运用简单随机抽样的实例吗?

学生回答：检验火柴的质量，灯的使用寿命，炸弹的破坏范围等．

问题8：通过以上的学习，你能说明一下简单随机抽样有哪些好处吗?

学生回答得合理即可，如：简单随机抽样较为省时省力，对总体的情况可以起到一个估计 的作用．

（教学说明：本环节设计的问题是为了引导学生经历数据处理的过程，所以教师要留给学生一定的时间和空间，要努力让所有学生都能参与到设计的活动中去，在活动的过程中建立统计观念．本环节的问题都有一定的开放性，教师要关注学生的结论，适时加以引导，特别是问题6中出现简单随机抽样的概念后，老师要让学生明白，用简单随机样本估计总体时，样本是总体的一部分，样本中喜爱种类节目的比例不是总体的比例，所得出的百分比只能用来估计总体的情况．）

三、巩固训练 熟练技能

（设计说明：通过基础练习，进一步感受抽样调查的实用性．）

练习1.下列调查方式合适的是（ ）

A. 要保证“神舟六号”载人飞船成功发射，对重要零部件采用抽查的方式

B．要了解中央电视台“新闻联播”节目的收视率，采用普查的方式

C. 要了解外国运动员对“奥运村”的满意度，采用抽样调查

D. 要了解一批灯泡的使用寿命，采用普查的方式

学生：选择C.

练习2.一次考试约20000名考生，从中抽取500名考生的成绩进行分析，这个问题的样本是（ ）

A．500 B．500名

C．500名考生 D．500名考生的成绩

学生：选择D．

练习3．指出下列调查中的总体、个体、样本和样本容量．

（1）从一批电视机中抽取20台，调查电视机的使用寿命．

（2）从学校七年级中抽取30名学生，调查学校七年级学生每周用于数学作业的时间．

学生：（1）总体是这一批电视机的使用寿命，个体是每台电视机的使用寿命，样本是20台电视机的使用寿命，样本容量是20．

（2）总体是学校七年级学生每周用于数学作业的时间，个体是学校七年级每名学生每周用于数学作业的时间，样本是30名学校七年级学生每周用于数学作业的时间，样本容量是30．

（教学说明：这三道练习题的设立是为了考查学生对抽样检查的掌握情况，特别是对抽样抽查中的总体、个体、样本及样本容量的理解．）

四、反思总结 情意发展

（设计说明：围绕三个问题，师生以谈话交流的形式，共同总结本节课的学习收获。）

问题1：本节课你学习了什么?

问题2：本节课你有哪些收获?

问题3：通过今天的学习，你想进一步探究的问题是什么?

（教学说明：以上设计再次通过对三个问题的思考引导学生回顾自己的学习过程，畅所欲言，加强反思、提炼及知识的归纳，纳入自己的知识结构）

五、课堂小结

1．本节主要学习抽样调查的方法．

3．注意的问题:

（１）只有在调查总体数目较多时才能使用抽样调查．

（２）抽样调查的总体、个体和样本都与调查的内容相联系，而样本容量只与样本的个体数有关．

六、布置作业

1、课本155页练习1、2、3；

（教学说明：及时作业是巩固课堂学习知识的重要环节，练习题主要训练学生对抽样调查的理解．）

七、拓展练习

（设计说明：在学习基础知识的基础上，拓展学生思维，提高学生的学习兴趣。）

练习1：下列问题适合抽样调查的个数是（ ）

①要了解一批炮弹的杀伤半径；②要了解一批鞭炮的爆炸百分率；③要了解某班学生的体重情况；④要了解2008北京奥运会的收视率；⑤要了解全国中小学生的视力情况．

A．4 B．3 C．2 D．1

学生：选择A．

练习2：为了了解某市老人的身体健康状况，在以下抽样调查中，你认为样本选择较好的是 （填序号）

①100位女性老人；②公园内100位老人；③在城市和乡镇先10个点，每个点任选10位老人．

学生：选择③.

（教学说明：本练习是以基础知识为主，出现非单一性的选择，以考查学生对抽样调查的理解．）

【评价与反思】

本节内容是在全面调查的基础上，增加调查人数，从而引出抽样调查．主要介绍简单随机抽样调查的方法及抽样调查中总体、个体、样本、样本容量的概念，属于探究课．

教材在学习了全面调查之后，以原有问题为基础，大幅增加调查的个体数量，从而引发学生探索更适宜的解决办法．整个过程前后呼应，过渡自然，使学生感受数学知识的连贯性，激发学生自主探索的意识．

教学设计上，虽然以自主探究学习为主，但对于某些学生从未接触过的概念，教师要适时给予说明和讲解，不仅要注重学生的交流合作，还要关注学生对新知识的理解情况，让学生在交流合作中发现数学的乐趣，在探究过程中提高数学的应用意识．