实数教学设计(二) 人教课标七年级下册

一、教学过程

(一)复习提问

1．有理数、无理数、实数的概念．

2．实数的分类．(两种方式)

例1 把下列各数写入相应的集合中：

以上内容应由学生自己先做，再由学生自己来纠正错误．教师再做适当提示。特别要注意有的学生一看不到不能化成有限小数的分类，如，就容易将其化入无理数，这说明学生在概念上还是不十分清楚，应让学生明白是分数就一定是有理数，必可化为有限小数或无限循环小数，要使学生清楚各概念之间的界限，抓住本质，区别相近的概念，

我们在讲解有理数概念的时候，接触过数轴的问题，请同学们回忆一下什么叫数轴?

我们知道规定了原点、正方向和单位长度的直线叫做数轴．每个有理数都在数轴上有自己相应的位置．反过来，同学们想一想数轴上所有的点是不是都表示有理数呢?下面我们来验证一下，首先画一个数轴：

以0到1为一边、单位长度为边长作一个正方形，以数轴的原点为圆心、正方形的对角线为半径画弧，根据勾股定理，我们知道这个正方形的对角线长为，所以所画的弧与数轴的正半轴的交点表示的数就是，由此我们看出数轴上的点表示的并不都是有理数，也有无理数．如果我们把所有的有理数连起来，组成的是一条断断续续的数轴，这其中的空缺就是我们刚刚学习的无理数，可见由有理数和无理数把整个数轴填充完整了，所以我们把这个数轴又称为实数轴．实数与数轴上的点是一一对应的．这其中包含着两层含义：第一，每一个实数都可以用数轴上的一个点来表示；第二，数轴上的每一个点都可以用一个实数来表示．

我们用数轴来表示实数，将数和图形联系在了一起，这给我们研究数学问题带来了方便，这也是我们数学中一个相当重要的数学思想——数形结合．

我们把实数表示在数轴上，最直观地表明了实数的大小，以原点为分界线，在原点的右侧，表示正数，在原点的左侧为负数，我们知道数轴上的实数从左到右是由小变大，并且数轴上的右侧的数总是比它左侧的数大，这就引出了实数比较大小的问题．显然同有理数之间的比较大小是类似的．

例2 比较大小：

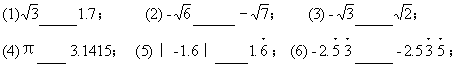
解：(1)“＞”我们前面计算时知道，化为小数再与1.7比较，便可

知答案了．可见在实数比较大小时，要经常用到无理数的近似值，所以有些常用的无理数的近似值应记住，如，，等，记住了，用时就方便些．

(2)“＞”作此题时，我们看到是两个负数比较大小，根据规则两个负数比较大小先比较他们的绝对值的大小，所以先比较与的大小，这两个无理数比较大小时，并不用将他们都化为小数，因为两个算术平方根比大小时，只需看他们的被开方数的大小就行了，被开方数大的，其算术平方根也大，这样我们就得到，再根据两负数比较大小，绝对值大的反而小的规律，我们就得到答案了．