实际问题与二元一次方程组 (第三课时)教学设计

§8.3 实际问题与二元一次方程组 (第三课时)

【教学重点与难点】

教学重点：用列表的方式分析题目中的各个量的关系，列二元一次方程组.

教学难点：从图表中获取有用信息，借助列表分析问题中所蕴含的数量关系

【教学目标】

1. 会用列表法分析应用题中的数量关系，列出相应的二元一次方程组解决较复杂的实际问题，并进一步提高解方程组的技能.

2. 通过探究3的学习，使学生学会从图表获取信息的方法，进一步感受设间接未知数与会解决问题的解题策略.

3.在解决问题的过程中，体会方程组是解决实际问题的重要模型.，发展学生的数学建模能力.

【教学方法】

教师将复杂问题分解成较简单的问题，给学生的探索设置低起点的台阶，创设和谐的学习环境，使学生对问题的探究一步步顺利展开.在问题解决的过程中，以学生自主探索、合作交流为主，教师引导、点拨为辅，努力使课堂成为个体主动思考、生生互动交流、师生互补提高的学习活动场所.

【教学过程】

一、创设情境 提出问题

（设计说明：利用一个较简单的问题，让学生逐步学习如何从图表中获取有用信息，进一步熟悉列二元一次方程组解应用题的方法，训练运算的速度与准确度.）

导语：前面我们利用二元一次方程组解决的许多实际问题，这些问题的条件是用文字语言给出的.还有些问题，条件由文字、图表共同给出，这就需要我们能读懂图表.这里给大家准备了一个比较简单的问题，请认真思考，独立解答.

问题：（2008海南）根据北京奥运票务网站公布的女子

双人3米跳板跳水决赛的门票价格（如表1），小明预

定了B等级、C等级门票共7张，他发现这7张门票的

费用恰好可以预订3张A等级门票.问小明预定了B等

级、C等级门票各多少张?

解：设小明预订了B等级，C等级门票分别为x张和y张.

依题意，得

解这个方程组得

答：小明预订了B等级门票3张，C等级门票4张.

（教学说明：教师提出问题，学生尝试解答，一名学生板演，结合板演订正，提醒学生注意过程的规范与运算的准确．）

二、探索新知 解决问题

问题：教材106页探究3

如图，长青化工厂与A，B两地有公路、铁路相连．这家工厂从A地购买一批每吨1 000元的原料运回工厂，制成每吨8 000元的产品运到B地．公路运价为1. 5元（吨·千米），铁路运价为1.2元（吨·千米），这两次运输共支出公路运费15000元，铁路运费97200元．这批产品的销售款比原料费与运输费的和多多少元?

SHApE \* MERGEFORMAT

1.总揽 题意，分析数量关系

（设计说明：由于探究3 题目较长，数量关系比较多且不易理清，所以先通过几个问题引导学生准确把握题意，找出题目中的等量关系，为列方程组解决问题扫清障碍）

问题1：要解决的问题是什么?

这批产品的销售款-（原料费＋运输费）=?

根据题目条件，运输费=15000＋97200，销售款、原料费都不能直接求出.

问题2 ： 产品的销售款、原料费、 运输费与那些量有关?是什么关系?

销售款=产品数量×产品单价，原料费=原料数量×原料单价，

运输费=路程×运价×货物重量

销售款与产品数量、销售单价有关，原料费与原料数量、原料单价有关，而公路运费和铁路运费与产品数量和原料数量都有关．因此需要先求出产品数量和原料数量.若设产品重x吨，原料重y吨，填写下表分析数量关系

由表中内容及题目条件可以得出：

铁路运费=1.2(110x＋120y)=97200

公路运费=1.5(20x＋10y)=15000

求出x,y的值以后，原料款1000y,销售款8000x可求，于是问题获解.

（教学说明：教师提出问题，学生思考、交流之后师生共同得出结论.学生回答问题时，要把理由交代清楚，尤其是自己的思考过程，以便学生之间相互学习.）

2.思考内化，解决问题

（设计说明：在师生讨论交流之后，让学生写出规范的解答过程，一方面进一步熟悉分析问题的方法及题目中的数量关系，另一方面训练规范的解答格式及运算的速度、准确度）

解：设产品重x吨，原料重y吨，根据题意得

解这个方程组，得

即产品重300吨，原料重400吨

所以销售款－原料费－运输费

=8000×300-1000×400-15000-97200=1887800

答：这批产品的销售款比原料费与运输的和多1887800元.

（教学说明：学生独立解答，一名同学板演.教师巡视时，及时为学习有困难的同学提供帮助.解答完毕，结合板演订正，并进一步引导学生思考：通过探究3的解决，你学到了哪些方法?在以后的学习中需要注意些什么?）

3.回顾反思：

（设计说明：结合具体问题梳理总结，学生的思路容易打开，且感触较深，有利于学生将新旧知识融合为一体，构建新的知识体系）

结合探究3中列方程组解决实际问题的过程，思考下面的问题：题目中的数量关系比较复杂时如何处理?什么时候间接设未知数?

（教学说明：学生结合解决问题的具体过程思考总结，教师视情况进行引导或提炼.）

三、巩固训练 熟练技能

（设计说明：通过解答下面的问题，进一步训练学生从图表中获取信息的能力，以及分析、解决实际问题的能力）

练习题：一批货物要运往某地，货主准备租用汽车运输公司的甲、乙两种货车，已知过去两次租用这两种货车的情况如下表：

现租用该公司3辆甲种货车及5辆乙种货车一次刚好运完这批货,如果按每吨付运费30元计算,你能算出货主应付运费多少元吗?

思考：要解决的问题是什么?为解决这个问题，首先要求出那些量?

经过思考交流明确：

最后的问题是求货主应付运费多少元，为此先应求出这批货物有多少吨，所以必须先求出甲、乙两种货车一次分别运货是多少吨.

分析：从表格中可以知道：2辆甲种货车与3辆乙种货车一次可运货物15.5吨，

5辆甲种货车与6辆乙种货车一次可运货物35吨

若设甲种货车一次运货x吨，乙种货车一次运货y吨,则 可以列出方程组

2x＋3y=15.5

5x＋6y=35

求出x,y的值以后，货主应付运费30（3x＋5y）就可以求出.

解：设甲种货车一次运货x吨，乙种货车一次运货y吨, 则货主应付运费30（3x＋5y）元，根据题意得

2x＋3y=15.5

5x＋6y=35

解得

x=4

y=2.5

∴货主应付运费30（3x＋5y）=30(3×4＋5×2.5)=735(元)

（教学说明：出示问题后，利用“思考”引导学生分析解题策略，先从总体上把握题目后写解答过程.完成后及时交流订正，将问题在课堂彻底解决.）

四、反思总结 情意发展

（设计说明：围绕三个问题，师生以谈话交流的形式，共同总结本节课的学习收获。）

问题1：本节课你学习了什么?

问题2：本节课你有哪些收获?

问题3：通过今天的学习，你想进一步探究的问题是什么?

（教学说明：以上设计再次通过对三个问题的思考引导学生回顾自己的学习过程，畅所欲言，加强反思、提炼及知识的归纳，纳入自己的知识结构）

五、课堂小结

1．本节主要学习从图表中获取信息及利用列表法分析数量关系，进而利用二元一次方程组解决实际问题.

2．主要用到的思想方法是方程思想：将实际问题转化成二元一次方程组解决

3．注意的问题:

（１）读懂图表的含义，从中获取有用信息.

（２）根据题目特点确定直接设未知数或间接设未知数

（３）解出方程组时要选择适当的方法，运算速度要快，准确度要高.

六、布置作业

1.必做题：课本108页习题 6，8

2.选做题：课本119页复习题9，10

（教学说明：及时作业是巩固课堂学习知识的重要环节，练习题主要训练列方程组解应用题的能力）

七、拓展练习

（设计说明：在学习基础知识的基础上，拓展学生思维，提高学生的学习兴趣。）

1. （2007上海市）2001年以来，我国曾五次实施药品降价，累计降价的总金额为269亿元，五次药品降价的年份与相应降价金额如下表所示，表中缺失了2003年、2007年相关数据．已知2007年药品降价金额是2003年药品降价金额的6倍，结合表中信息，求2003年和2007年的药品降价金额．

解：[解法一]设2003年和2007年的药品降价金额分别为亿元、亿元．

根据题意，得

解方程组，得

答：2003年和2007年的药品降价金额分别为20亿元和120亿元．

[解法二]设2003年的药品降价金额为亿元，

则2007年的药品降价金额为亿元．

根据题意，得．

解方程，得，．

答：2003年和2007年的药品降价金额分别为20亿元和120亿元．

2. （2007恩施自治州）团体购买公园门票票价如下：

今有甲、乙两个旅行团，已知甲团人数少于50人，乙团人数不超过100人.

若分别购票，两团共计应付门票费1392元，若合在一起作为一个团体购票，总计

应付门票费1080元．

(1)请你判断乙团的人数是否也少于50人．

(2)求甲、乙两旅行团各有多少人?

解：（1）∵100×13＝1300<1392

∴乙团的人数不少于50人，不超过100人

（2）设甲、乙两旅行团分别有x人、y人，

则

解得：

所以甲、乙两旅行团分别有36人、84人

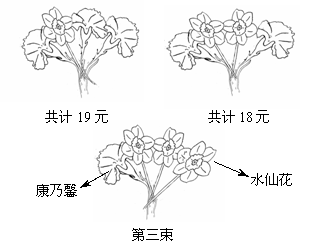
3.（2008济南）教师节来临之际，群群所在的班级准备向每位辛勤工作的教师献一束鲜花，每束由4支鲜花包装而成，其中有象征母爱的康乃馨和象征尊敬的水仙花两种鲜花，同一种鲜花每支的价格相同．请你根据第一、二束鲜花提供的信息，求出第三束鲜花的价格．

．解：设康乃馨每支元，水仙花每支元

由题意得：

解得：

第三束花的价格为

答：第三束花的价格是17元．

（教学说明：教学时可根据实际做调整，要让学生充分的合作交流，共同解决问题）

【评价与反思】

本课是实际问题与二元一次方程组的最后一节课，问题更加贴近现实生活，解决的难度明显加大.为让学生能从总体上准确把握题意，一方面设计部分思考题引导学生讨论交流，另一方面利用表格将题目中的数量关系清晰的呈现出来，学生踏着这些台阶，一步步找到了解决问题的途径.

由于本课涉及内容丰富，如何突出重点、突破难点成为这节课能否成功的关键.为此，开始先设计一个简单题目做准备，将获取图表信息这一问题提前处理；在探究3中重点是利用表格分析复杂的数量关系，练习题则是对探究3的进一步巩固和对本课学习效果的检测.这样，的学习过程符合学生的认知规律，能达到学习目标.