生活中的平移2 人教课标七年级下册
课题 | 8.1 生活中的平移 | 课型 | 新授 | ||
教 学 目 标 | 知识目标: 经历观察、分析、操作、欣赏及抽象、概括等过程,探索图形平移的基本性质。 通过具体实例认识平移,理解平移的基本性质,并能应用解决相关的问题。 能力目标: 进一步提高学生观察分析、归纳总结的能力,发展空间观念。 德育目标: 进一步培养学生小组合作、团结互助的品质,增强审美意识。 | 教学重点 | 知识目标 | ||
教学难点 | 平移性质的总结 | ||||
教法 | 引导发现 | ||||
学法 | 小组合作、探究讨论 | ||||
教具 | 投影仪 | ||||
授课教师 | |||||
教学内容 | 教学手段 | 教学建议 | 教学评价 | ||
引入: 小时候,你喜欢游乐园里的哪些游戏?你想过没有,小火车在笔直的铁轨上开动时,火车头走了200米,车尾走了多少米? 你坐过电梯吗?它是如何运动的?你见过老井上的辘轳吗?打水时,哪些物体在动?如何动的? 其实,数学就在我们身边,它有很多规律等待我们去探索、去发现。无论是微观世界的粒子运动,还是浩瀚宇宙中的行星运动,其中最简捷的运动变化形式主要是平移与旋转。 | 教师提出问题,学生各抒己见 | 通过实际生活中的一些常见现象引起学生思考,从而引入课题。 对于辘轳,学生可能没见过,可引导学生观察p56的图。 | 学生的回答只要合理,就应给与肯定。 | ||
新知探索: 1、p57、图3—1及问题。 2、平移:在平面内,将一图形沿某个方向移动一定的距离,这样的图形运动称为平移。 平移不改变图形的形状和大小。 在图3—2中,点A、B、C、D分别平移到了点E、F、G、H,A与E,B与F,C与G,D与H分别是一对对应点,AB与EF是一对对应线段;∠BAD与∠FEH是一对对应角。 | 学生看书思考并回答问题。 教师反馈矫正。 教师也可以以学生常见的平移实例引入平移的概念。 学生找出其它的对应线段、对应角 | 由图3—1中传送带上的电视机和手扶电梯上的人的运动引入平移的概念。 平移的特征:图形上的每一个点都沿同一方向移动了相同的距离;平移不改变图形的形状和大小。 | 鼓励学生大胆阐述自己的观点。 | ||
教 学 内 容 | 教学手段 | 教学建议 | 教学评价 | ||
p58、想一想 平移的性质:经过平移,对应点所连的线段平行且相等;对应线段平行且相等,对应角相等。 | 学生自主探索,小组合作交流,师生共同订正完成。 | 1、鼓励学生大胆地用自己的语言描述性质。 2、问题3中,图中有些相等关系并不是通过平移产生的。 3、可将对应点所连的线段若在同一条直线上作为一种特例。 | 关注学生对问题的归纳总结能力和语言表达能例。 | ||
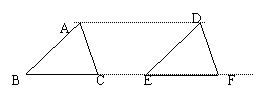
p58、例1 p59、随堂练习1、2 p60、试一试 如图,△ABC经过平移得到的△DEF,则图中平行且相等的线段有_________∠BAC= ∠________,∠ACB=∠_______ 如图,平移方格纸中的图形,使点A平移到A/处,画出平移后的图形。 | 学生自主探索,反馈矫正 | 1、要尽量让学生自己独立完成,鼓励学生之间互相纠错。 2、例1中,要求学生说出根据。 | 鼓励学生敢于暴露错误的思维过程。 | ||
四、课堂小结: 本节课你学会了哪些知识? | 学生归纳,教师适当补充。 | 可从以下两方面引导: 1、本节课有哪些新的收获。 2、本节课还有什么疑问。 | 鼓励学生各抒己见,只要符合本节课的精神,就应鼓励。 | ||
五、作业:p59、习题3.1 1、2、3 设计一幅由平移得到的优美图画。 | |||||
课题 | 8.3 生活中的旋转 | 课型 | 新授课 | |||
说课人 | 时间 | |||||
目
标
| 1、经历对生活中与旋转现象有关的图形进行观察、分析、欣赏,以及 动手操作、画图等过程,掌握有关画图的操作技能,发展初步的审美能力,增强对图形欣赏的意识。 2、通过具体实例认识旋转,理解旋转前后两个图形对应点到旋转中心的距离相等、对应点与旋转中心的连线所成的角彼此相等的性质。 | |||||
重点 | 通过具体实例认识旋转,理解旋转前后两个图形对应点到旋转中心的距离相等、对应点与旋转中心的连线所成的角彼此相等的性质。 | |||||
难点 | 会用所学知识分析生活中的旋转现象 | |||||
教法 | 观察探究、动手实践、合作交流。 | |||||
教具 | 学具盒中的图形 | |||||
教
学
过
程
| 教学内容 | 教学活动 | 教学建议 | 教学评价 | ||
一、引例
二、旋转的定义及有关概念 | 观察课本 上图情景中的转动现象,有什么共同特征? 钟表的指针、钟摆在转动过程中,其形状、大小、位置是否发生改变?汽车方向盘的转动呢? 在平面内,将一个图形绕一个定点沿某个方向转动一个角度,这样的图形运动成为旋转,这个定点称为旋转中心,转动的角称为旋转角,旋转不改变图形的大小和形状。 | 引导学生用数学的眼光看待生活中的有关问题,进一步发展学生的数学观,使学生学到活生生的数学。 使学生结合具体情景中理解旋转的含义,切忌死记硬背。 | 关注学生参与数学活动的主动程度和合作交流的意识与能力。 关注学生在具体情景中识别旋转现象。 | |||
教学内容
议一议
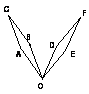 如图,如果把钟表的指针看做四边形AOBC,它绕O点旋转得到四边形DOEF,在这个旋转过程中:
如图,如果把钟表的指针看做四边形AOBC,它绕O点旋转得到四边形DOEF,在这个旋转过程中:
旋转中心是什么?旋转角是什么?
旋转中心是O, 旋转角是∠AOD或∠COF或∠BOE
经过旋转,点A、B分别移动到什么位置?
经过旋转,点A移动到点D,点B移动到点E
AO与DO的长有什么关系?BO与EO呢?
AO=DO BO=EO
∠AOD与∠BOE有什么大小关系?
∠AOD=∠BOE
旋转的性质
上图中,点D、E、F分别是A、B、C的对应点。经过旋转,图形上的每一点都绕旋转中心沿相同方向转动了相同的角度。
任意一对对应点与旋转中心的连线所成的角都是旋转角,对应点到旋转中心的距离相等。
 钟表的分针匀速旋转一周需要60分
钟表的分针匀速旋转一周需要60分
![]() 指出它的旋转中心
指出它的旋转中心
经过20分钟,分针旋转了多少度?
解:(1)它的旋转中心是钟表的轴心
(2)分针匀速旋转一周需要60分,因此旋转20分,
分针旋转的角度为![]()
做一做
观察图形,图中正方形ABCD与正方形EFGH边长相等,
E
A D
F H
B C
G
 这个图案可以看做是哪个“基本图案”通过旋转得到的?
这个图案可以看做是哪个“基本图案”通过旋转得到的?
鼓励学生用多种方法解决。描述中注意1)基本图形2)旋转中心3)旋转角4)旋转方向
六、本节课了解到那些关于旋转的知识
七、作业:
八、教学反思
8·4 简单的旋转作图
课题 | 8.4 简单的旋转作图 | 课型 | 新授课 | |||
说课人 | 时间 | |||||
教学目标
| 经历对具有旋转特征的图形进行观察、分析、动手操作、画图等过程,掌握有关画图得操作技能。 2、能够按要求作出简单平面图形旋转后的图形。 | |||||
重点 | 能够按要求作出简单平面图形旋转后的图形。 | |||||
难点 | 能够按要求作出简单平面图形旋转后的图形。 | |||||
教法 | 观察探究、动手实践。 | |||||
教具 | ||||||
教
学
过
程
| 教学内容 | 教学活动 | 教学建议 | 教学评价 | ||
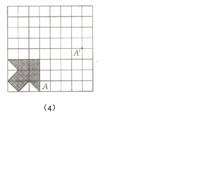
一、p69引例 在方格纸上作出“小旗子”绕O点按顺时针方向旋转90o后的图案,并简述理由
| 观察交流,联想, 做出图形 学生分组讨论,然后自己总结方法 | 建议如下: (1)“小旗子”是结构特别简单的平面图形,它的边缘由简单的线段所连成,而且边缘上的关键点仅仅四个。 (2)在方格纸上旋转90o,旋转后的图形恰落在格子点上。 (3)以简单的例子作为本节的导入,符合教学目标的要求。 (4)教师总结 | 学生只要说的合理即可。 | |||
二、例1。 p69例1 | 分析:假设顶点B、C的对应点分别为点 E、F,则,∠BOE,∠COF,∠AOD都是旋转角, 且OE=OB,OF=OC | 建议如下: 教师给出图形,先让学生交流。 要重视对“分析”的处理,这是使学生明确“作图”道理的重要途径 可以让学生讨论多种方法,但是重点讲书上例1的方法,让学生切实掌握。 明确:旋转中心、旋转方向、旋转角 小结:旋转作图的方法 找关键点 2、作角相等 3、截线段相等 4、按原方式连结 | 关注学生参与数学活动的主动程度和合作交流的意识与能力。 | |||
中考 高考名著
常用成语
 三、达标练习:
三、达标练习: