三元一次方程组解法举例 教学设计

§8.4 三元一次方程组解法举例

教材分析

本课的主要内容是学习三元一次方程组的解法，由于三元一次方程组相关知识与二元一次方程组类似，所以先结合实例运用类比法学习三元一次方程组的有关概念，然后利用消元思想解三元一次方程组.尽管三元一次方程组与二元一次方程组的解法有许多类似之处，毕竟三元一次方程组复杂得多，所以在学习的过程中，重点处理好与二元一次方程组解法中不同的环节，在比较的过程中学习新知识，使学生对消元思想有更深层次的认识，能将这种思想迁移到解决四元一次方程组、五元一次方程组……等问题中.

列三元一次方程组解决实际问题虽然不是这节课的重点，不过它有助于学生理解为什么要学习一元高次方程组的解法以及数学与生活的密切联系，同时也可以为以后学习二次函数做一些准备，所以有必要做一部分较简单的实际应用题.

在理解运用消元思想方法的同时，观察分析及运算能力也是这节课训练的重点内容，注意在应用的过程中培养学生的良好思维、表达习惯.

【课时分配】1课时

【教学重点与难点】

教学重点：会准确、迅速地解三元一次方程组

教学难点：根据方程组的特点确定先消哪个元，怎么消?

【教学目标】

1. 会用代入消元法和加减消元法解三元一次方程组，提高运算技能.

2. 通过解三元一次方程组，进一步体会“消元化归”思想.

3. 通过学习体会前后知识之间、数学与生活之间的密切联系，发展应用意识.

【教学方法】

利用一个具体问题，在复习已有知识的基础上类比学习学习新内容.教师为学生提供部分学习素材，创设和谐融洽积极向上的学习氛围，学生在独立思考的基础上与同学交流合作，教师的指导与学生的探索有机结合，使学生在尝试中发展、提高.

【教学过程】

一、创设情境 提出问题

（设计说明：利用一个既能用二元一次方程组解决，又能用三元一次方程组解决的问题，让学生在解决问题的过程中，自然过渡到新知识的学习.）

导语：通过以上几节课的学习，我们不仅知道了什么是二元一次方程、二元一次方程组，而且还能利用他们来解决许多实际问题，这些问题中的未知数有两个.如果问题中的未知数多于两个，你能解决吗?请大家尝试解决下面的问题.

问题：小明手头有12张面额分别为1元、2元、5元的纸币，共计22元，其中1元的纸币的数量是2元纸币数量的4倍.求1元、2元、5元纸币各多少张?

解法一：设1元、2元、5元的纸币分别为x张、y张，则5元的纸币（12-x-y）张，根据题意得 x＋2y＋5(12-x-y)=22

x=4y

解得

x=8

y=2

∴12-x-y=12-8-2=2

答：1元、2元、5元的纸币分别有8张，2张，2张.

解法二：设1元、2元、5元的纸币分别为x张、y张、z张

根据题意，得：

x＋y＋z=12 ①

x＋2y＋5z=22 ②

x=4y ③

多数同学会列二元一次方程组解答，也可能会有同学列出三元一次方程组，教师注意观察，请学生介绍自己的想法及遇到的问题.如果没有学生列三元一次方程组，教师可以提出问题：如果设三个未知数，会得到那些关系式?结合具体式子学习三元一次方程组的相关知识.

（教学说明：教师提出问题，学生尝试解决，教师结合学生的具体情况灵活调控：或顺势进入新课学习，或提出新的问题将学生引导到先课内容上来．）

二、探索新知 解决问题

1.三元一次方程组的有关概念：

（设计说明：结合实例，用类比法学习三元一次方程族的有关概念）

（1） 三元一次方程

结合前面得到的三个方程学习相关概念

x＋y＋z=12 ①

x＋2y＋5z=22 ②

x=4y ③

教师：大家知道，方程③是二元一次方程，方程①、②呢?你能说出它们的特点吗?

定义：含有三个未知数，并且含有未知数的项的次数都是1，这样的整式方程方程叫做三元一次方程

（2）三元一次方程组

这个问题的解必须同时满足上面三个条件，因此，我们

把这三个方程合在一起，写成

x＋y＋z=12

x＋2y＋5z=22

x=4y

这个方程组含有三个未知数，每个方程中含未知数的项的次数都 是1，并且一共有三个方程，像这样的方程组叫做三元一次方程组

（教学说明：由于三元一次方程组的概念比较容易理解，结合实例师生以谈话的方式解决即可）

过渡：如果能把三元一次方程组的解求出来，问题就解决了，那么这个方程组怎样解呢?请打家回顾几个问题：解二元一次方程组的基本思路是什么?-----消元，将二元方程组转化成一元一次方程具体方法是什么?------代入消元法、加减消元法， 能否用类似的方法解三元一次方程组呢?

2. 三元一次方程组的解法

问题1 解方程组

（设计说明：利用列出的方程组探索三元一次方程组的解法，体会消元思想的意义）

x＋y＋z=12 ①

x＋2y＋5z=22 ②

x=4y ③

(1) 指导思想：将三元一次方程组转化成二元一次方程组

（2）具体做法：通过①③消去未知数z，得到关于x,y的方程，与②组成二元一次方程组，先求出x,y,再求出z

（3）解答过程：①×5-②，得4x＋3y=38 ④

解由③④组成的方程组， x=4y ③

4x＋3y=38 ④

得

x=8

y=2

把x=8,y=2代入①，得 z=2

∴原方程组的解为

x=8

y=2

z=2

（教学说明：师生共同分析思路，有学生独立尝试写出解答过程，结合板演订正并梳理主要路子：必须先确定消去哪个未知数，然后将三元一次方程组转化为二元一次方程组，最后要写出方程组的解）

问题2 解三元一次方程组

3x＋4z=7 ①

2x＋3y＋z=9 ②

5x－9y＋7z=8 ③

（设计说明：由于这个方程组与问题1中的方程组解法类似，只是计算稍加复杂，所以利用它进一步熟悉解三元一次方程组的基本步骤，训练学生的观察能力及运算技能）

解：②×3＋③ ，得

11x＋10z=35 ④

①与④组成方程组

3x＋4z=7

11x＋10z=35

解这个方程组，得 x=5

z=-2

把x＝5，z＝-2代入②，得y=

因此，三元一次方程组的解为

x=5

y=

z=-2

（教学说明：学生独立完成，一名同学板演.结合出现的问题及时点评，使学生体会到思路清晰并不代表能做对，使学生养成认真、细心的良好习惯.）

问题3 在等式 y=ax²＋bx＋c中,当x=-1时,y=0;当x=2时,y=3;当x=5时,y=60.

求a,b,c的值

（设计说明：问题3是三元一次方程组的简单应用，利用这个题目，一方面让学生体会利用三元一次方程组可以解决问题，另一方面进一步探究三元一次方程组的一般解法，提高学生的观察分析能力与运算技能.）

分析：(1)根据题意，列出关于a，b，c的三元一次方程组，通过解方程组，求出a,b,c的值.

(2)方程组中的每一个方程都含有三个未知数，这是和前面的方程组不同的地方，因此它的解法也有所区别.由于c的系数最简单，所以先消去c.用②-①,③-①分别得到两个关于a,b的二元一次方程，解由它们组成的方程组就可以求出a,b,的值，然后再求出c的值.

解：根据题意，得三元一次方程组

a－b＋c= 0 ①

4a＋2b＋c=3 ②

25a＋5b＋c=60 ③

②－①， 得 a＋b=1 ④

③－①，得 4a＋b=10 ⑤

④与⑤组成二元一次方程组

a＋b=1

4a＋b=10

解这个方程组，得

a=3

b=-2

把 a=3 代入①，得

b=-2

c=-5

因此

a=3

b=-2

c=-5

答：a=3, b=-2, c=-5.

归纳：解三元一次方程组的一般步骤

1.观察方程组的系数特点，确定先消哪个未知数.

2.消元，得到一个二元一次方程组.

3.解二元一次方程组，求出两个未知数的值.

4.求出第三个未知数的值，写出方程组的解.

（教学说明：师生共同分析解题思路，然后由学生写出解答过程，最后归纳解三元一次方程组的一般步骤及注意事项.）

三、巩固训练 熟练技能

（设计说明：通过练习，掌握三元一次方程组的解法，形成初步运算技能）

教材114页练习1，2

（教学说明：独立完成，及时订正，注意解题的规范与计算的准确）

四、反思总结 情意发展

（设计说明：围绕三个问题，师生以谈话交流的形式，共同总结本节课的学习收获。）

问题1：本节课你学习了什么?

问题2：本节课你有哪些收获?

问题3：通过今天的学习，你想进一步探究的问题是什么?

（教学说明：以上设计再次通过对三个问题的思考引导学生回顾自己的学习过程，畅所欲言，加强反思、提炼及知识的归纳，纳入自己的知识结构）

五、课堂小结

1．本节主要学习三元一次方程组的解法.

2．主要用到的思想方法是消元思想：将三元一次方程组转化成二元一次方程.

3．注意的问题:

（１）先消哪个未知数，怎样消元，取决于方程组的系数特点，要仔细观察，选择较简单的方法.

（２）消元时，两次消去的必须是同一个“元”.

（３）解出方程组时要细心，在准确的基础上提高运算速度.

六、布置作业

1、必做题：课本114页习题1，2，3

2.选做题：课本115页习题4，5；119页复习题 11

（教学说明：及时作业是巩固课堂学习知识的重要环节，练习题三元一次方程组的解法）

七、拓展练习

（设计说明：在学习基础知识的基础上，拓展学生思维，提高学生的学习兴趣。）

1. 如果方程组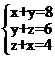的解使代数式kx＋2y -3z的值为10，则k＝（ ）

提示：解方程组求出x，y，z的值代入kx＋2y -3z=10即可求出k的值.

2. 有甲、乙、丙三种商品，如果购甲3件、乙2件，丙1件共需315元钱，购甲1件、乙2件、丙3件共需285元钱，那么购甲、乙、丙三种商品各一件共需 元钱．

提示：设甲、乙、丙三种商品的价格分别是x元，y元，z元，则

3x＋2y＋z=315①

x＋2y＋3z=285②

①＋②,得 4(x＋y＋z)=600

∴x＋y＋z=150

3.为确保信息安全，信息需要加密传输，发送方由明文对应密文（加密），接收方由密文对应明文（解密）已知加密规则为明文x，y，z对应密文为2x＋3y，3x＋4y，3z.例如：明文1，2，3对应密文8，11，9当接收方收到密文12，17，27时，则解密得到的明文为 解析：本题仔细分析一下可以知道这是一道三元一次方程组的问题，由题意可设这三个明文数字为x，y，z得 2x＋3y=12 x=3 3x＋4y=17 解得y=2 3z=27 z=9

所以，解密得到的明文为3，2，9

（教学说明：教学时可根据实际做调整，要让学生充分的合作交流，共同解决问题）

【评价与反思】

1.因需要而学习，在应用中发展：结合实际问题引入三元一次方程组的有关概念，为解决具体问题研究三元一次方程组的解法，掌握解法之后解决新的更多更复杂的问题，使学生头脑中建立这样的联系----学以致用

2.类比迁移，举一反三：类比二元一次方程组的知识学习三元一次方程组，并进一步应用于解其它一元高次方程组.同时，根据方程组的特点灵活选择恰当的解法，在应用的过程中形成技能技巧.