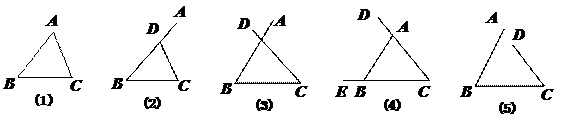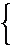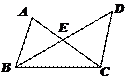三角形的边 教学设计
§17.1 与三角形有关的线段
教材分析
三角形是最常见的几何图形之一,在生产和生活中有广泛的应用.本节主要介绍与三角形的有关的线段(边、高、中线、角平分线)的概念和性质,使学生对三角形的有关知识有更为准确的理解.
三角形是认识其他图形的基础,学生在小学时已经学过有关三角形的一些知识,也了解三角形的许多性质,在第三章《图形认识初步》和第五章《相交线与平行线》中也学习了线段、平行线、相交线等有关知识,为本节的学习打下了基础.所以,在学习时,应注意让学生多与实际生活相联系,多与已经学过的知识相联系.由于在小学的学习中,图形的认识多以观察、测量为主,所以在学习三角形有关的线段的性质的时候,应注意培养学生的推理能力,所得到的每一个结论都要有依据,也为以后正式学习证明打下基础.
本节的重点是对三角形有关线段和三角形的稳定性的了解,难点是学生对三角形三边关系的理解和运用.在以往的学习中,“等量”是学习中最常见的关系,学生对等量关系的认识和运用较为熟练,这也就使学生在面对不等关系时有了一定的迷茫.所以,教师在帮助学生理解“三角形两边之和大于第三边”的同时,也要引导学生学会在怎样的环境中运用这种的性质.
在教学过程中,教师应注意把握教学要求.与三角形有关的一些概念在本章中只要求达到了解(认识)的程度就可以了,进一步的要求可通过后续学习达到.
【课时分配】3课时
§7.1.1三角形的边
【教学重点与难点】
教学重点:1.了解三角形的概念及分类,能从图中识别三角形,并能用符号语言表示出来.
2.通过具体的实践活动,理解三角形三边的不等关系.
教学难点:1.对三角形概念的理解.
2.在具体的图形中不重复,且不遗漏地识别所有三角形.
3.三角形三边不等关系的应用.
【教学目标】
1.了解三角形的概念,学会用符号语言表示三角形.毛
2.通过具体的实践活动理解三角形三边的不等关系.
3.引导学生通过实验探究三角形的稳定性,培养学生独立思考的学习习惯和动手能力.
【教学方法】
创设情境,从学生已学内容出发,引导学生积极探索,发现问题,并能通过实践解决问题.教学环节的设计与展开,都从实际生活出发,以已学内容为基础,引导学生通过观察、实践、想象、推理、交流等活动发现并解决问题,培养学生良好的学习作风和学习习惯.
【教学过程】
一.创设情境 提出问题
(设计说明:通过展示现实生活中建筑的图片,让学生从常见图形入手,降低知识难度,激发学生自主学习的兴趣和积极性,并引入新课.)
问题1:观察下面的图片,你能找到哪些我们熟悉的图形?
|
学生回答:三角形、四边形等.
问题2:在小学,我们学过三角形,你了解三角形的哪些性质?
(教学说明:教师所提出的问题,可以引导学生回顾已学过的相关知识,同时在教学中要注意引导学生对已有知识进行深入思考,从而发现问题.)
二、探索新知 解决问题
1.观察三角形的构成,探索三角形的概念
(设计说明:通过动手操作和观察来引导学生对三角形进行更深入的探索)
问题1:你能画出三角形吗?
让学生画出三角形,直观感受三角形的构成.
问题2:结合你画的三角形,说明三角形是由什么组成的?
学生回答:三角形是由三条线段组成的.
问题3:下面的几个图形都是由三条线段组成的,它们都是三角形吗?
|
学生回答:只有第(1)个是三角形,其他的都不是.
问题4:什么叫三角形?
学生回答,师归纳:由不在同一直线上的三条线段首尾顺次相接所组成的图形叫做三角形.
(教学说明:三角形的概念,学生在小学只是结合图形说明三角形是由三条线段组成的,但在这里要进一步严格定义,特别要强调“首尾顺次相接”.所以本环节设计了阶梯式的问题,引导学生经历了动手画图、回顾旧知、观察区分、归纳总结四个过程.在问题3中,要使学生明白,(2)(3)(4)不是单一的三角形,而是三角形与线段的组合图形.在归纳总结时,要留给学生一定的时间进行思考和归纳,教师也要适时进行引导和强调.)
2.自主学习三角形的表示方法及分类
(设计说明:自学三角形的表示方法,并能在具体的图形中不重不漏地识别所有三角形)
|
问题1:根据右图回答以下问题:
(1)在三角形中,什么叫边?什么叫内角?什么叫顶点?
(2)三角形有几条边?有几个内角?有几个顶点?
(3)如何用符号表示三角形ABC?
(4)如何用小写字母表示三角形ABC的三条边?
学生回答:组成三角形的三条线段都叫做三角形的边;相邻两边所组成的角叫做三角形的内角,简称三角形的角;相邻两边的公共端点是三角形的顶点.三角形有三条边,三个内角,三个顶点.三角形ABC用符号表示为△ABC.△ABC的边AB为顶点C所对的边(∠C所对的边),可以用顶点C的小写字母c 表示,同样,边AC可用b表示,边BC可用a表示.
问题2:如果将三角形分类,按照边的关系分可以分成几类?按角的关系又如何分类呢?
学生回答:三角形按照“有几条边相等”可以分为:
![]() 等边三角形
等边三角形
三角形 等腰三角形
不等边三角形
也可以按照边的相等关系分为:
![]() 不等边三角形
不等边三角形
![]() 三角形 底边和腰不相等的等腰三角形
三角形 底边和腰不相等的等腰三角形
等腰三角形
等边三角形
![]() 三角形按照角的关系可以分为:
三角形按照角的关系可以分为:
![]() 直角三角形
直角三角形
三角形 锐角三角形
斜三角形
 钝角三角形
钝角三角形
问题3:如图,找出图中的三角形,用符号表示出来,
并指出AB、AD、CD分别是哪个三角形的边.
学生回答:图中共有三个三角形,分别是△ABC、△ABD、△ADC,其中AB既是△ABC的边,也是△ABD的边,AD既是△ABD的边,也是△ADC的边,CD是△ADC的边.
(教学说明:对于三角形的边、角和顶点,学生在小学已经接触过,所以只要理解它们的意义即可,不要求背定义.在表示方法上要注意强调,在表示△ABC时,三个顶点字母A、B、C的顺序可以改变,所以△ABC、△ACB、△BAC、△BCA、△CAB、△CBA表示的是同一个三角形.同时,要让学生明白,并不是所有的图形都可以用符号表示,目前只有角和三角形可以分别用“∠”和“△”表示.对于三角形的分类,教师要加以引导,启发学生进行思考.在分类时,只要分得合理就要给予肯定,并利用这一机会让学生了解“分类思想”.问题3虽然比较简单,但通过这个练习,不仅巩固了所学的知识,同时也要教会学生找三角形的规律.)
3.通过观察实践,理解三角形三边关系
(设计说明:通过观察与实践,经历猜想与推论的过程,理解三角形三边的不等关系.)
|
学生回答:小虫从B出发沿三角形的边爬到C有2条线路:
(1)从BC,即线段BC的长;
(2)从BAC,即线段BA与线段AC长之和:BA+AC.
经过测量可得BA+AC>BC,所以这两条线路的长不一样.
根据“两点的所有连线中,线段最短”,说明BA+AC>BC.
问题2:联系三角形的三边,从问题1中你可以得到怎样的结论?
学生回答:三角形两边的和大于第三边.
问题3:用三条长度分别为5、9、3的线段能组成一个三角形吗?为什么?
学生回答:用三条长度分别为5、9、3的线段不能组成一个三角形,因为5+3<9.
(教学说明:在探究问题1的时候,教师要留给学生一定的时间进行思考和讨论,同时要引导并启发学生运用各种不同的方法说明结论的正确性,最终的目的是让学生体会推理的严谨性.我们知道,由“三角形两边的和大于第三边”可以得出“三角形两边之差小于第三边”这样的结论,但这种变化要运用不等式的基本性质,所以等学生在第九章学了不等式的基本性质之后再作介绍,这里不必扩展讲解.问题3的设立是为了让学生明白,“三角形两边的和大于第三边”可以用来判断三条线段能否组成三角形,同时要强调,能够组成三角形的三条线段必须满足这个结论,这也是三角形三边关系的应用范围.在解答时,学生有时会只因为5+9>3错解为能够组成三角形,所以教师要强调对于这三个长度,只有在任意两个长度之和都比第三个大时,才能够组成三角形.为了使判断方法简便一些,教师可以引导学生进行思考,得到只要检查较小的两边的和是否大于第三边就可以了.)
三、巩固训练 熟练技能
(设计说明:通过渐进式的练习,帮助学生进一步加深对三角形的认识,形成初步技能.)
练习1.在角形是指( )
A.由三条线段所段组成的封闭图形
B.由不在同一直线上的三条直线首尾顺次相接的组成的图形
|
D.由三条线段首尾顺次相接的组成的图形
学生:B.
练习2.图中有几个三角形?用符号表示这些三角形.
学生:共有5个三角形.
分别是:△ABC、△BCD、△BCE、△ABE、△CDE
练习3.有三根木棒长分别为3cm、6cm和4cm,用这些木棒能否围成一个三角形?为什么?
学生:能,因为3+4>6.
练习4.用一条长18 cm的细绳围成一个等腰三角形.
(1)如果腰长是底边的2倍,那么各边的长是多少?
(2)能围成有一边的长为4 cm的等腰三角形吗?为什么?
学生:解:(1)设底边长为x cm,则腰长2x cm.
x +2x +2x =18,
解得x =3.6.
所以,三边长分别为3.6 cm,7.2 cm,7.2 cm.
(2)因为长4 cm的边可能是腰,也可能是底边,所以需要分情况讨论.
如果长的边为底边,设腰长为x cm,则
4+2x=18,
解得x =7.
如果长4 cm的边为腰,设底边长为x cm,则
2×4+ x =18,
解得x =10.
因为4+4<10,出现两边的和小于第三边的情况,所以不能围成腰长是4 cm的等腰三角形.
由以上讨论可知,可以围成边长是4 cm的等腰三角形.
(教学说明:从基础出发,加深认识.解答练习3时注意,不必比较三次,只要两条较小的长度之和大于最大长度就可以了.练习4中要让学生注意“有一边的长”并没有指明这一边是腰还是底,所以要分情况讨论,同时所求出的三个长度要能够组成三角形.)
四、反思总结 情意发展
(设计说明:围绕三个问题,师生以谈话交流的形式,共同总结本节课的学习收获。)
问题1:本节课你学习了什么?
问题2:本节课你有哪些收获?
问题3:通过今天的学习,你想进一步探究的问题是什么?
(教学说明:以上设计再次通过对三个问题的思考引导学生回顾自己的学习过程,畅所欲言,加强反思、提炼及知识的归纳,纳入自己的知识结构)
五、课堂小结
1.本节主要学习三角形的概念、表示方法及三角形三边的关系.
2.本节涉及到的思想方法是分类思想.
3.注意的问题:
(1)在三角形的概念中要注意两点:①不在同一直线上;②首尾顺次相接.
(2)判断三条线段能否组成三角形,一定要检查是否任意两边之和都大于第三边.
六、布置作业
1、课本69页习题7.1的1、2、;
(教学说明:及时作业是巩固课堂学习知识的重要环节,练习题是针对本节的重、难点进行巩固.)
七、拓展练习
(设计说明:在学习基础知识的基础上,拓展学生思维,提高学生的学习兴趣。)
练习1:下面各组数中不能构成三角形的一组数是( )
A.0.2,0.6,0.7 B.5k,7k,10k (k≠0)
C.m-a,m,m+a (m·a≠0) D.1,1,33
学生:选择C.
练习2:小明想要钉一个三边长都是整数的三角形,现在他只有两根分别长4cm和5cm的木条,那么第三根木条的长度可以是多少?(写出所有可能结果)
学生:第三根木条长可以是2cm、3cm、7cm、5cm、6cm、7cm、8cm.
练习3:平面上有四个点A、B、C、D,用它们作顶点可以组成几个三角形?
学生:由于题中并没有说明这四个点是否在同一条直线上,所以要分情况讨论.
(1)四点共线时,不能组成三角形.
(2)三点共线时,可以组成三个三角形.
(3)任意三点都不共线时,可以组成四个三角形.
(教学说明:这三个练习都含有不定因素,所以要让学生充分的合作交流,共同解决问题,特别是练习3,情况较多,教师可以适时加以引导.)
【评价与反思】
本节内容是七年级数学第七章的第一节,主要介绍三角形的概念、表示方法及三角形三边的关系,是一节概念教学课.
本节的知识内容是在学生已经学习了一部分有关三角形的知识的基础上,对三角形进行更深入的研究.在教学过程中,教师不断引导学生从已有的知识为出发点进行深入思考,从而发现问题.学生解决问题要以独立思考为主,当遇到困难时要学会求助和交流,教师也要留给学生充分的思考与交流的时间,让学生能够经历得出结论的过程,以培养学生发现问题和解决问题的能力.
在教学设计上,关注学生自主学习、独立思考的能力,并让学生懂得求助,注重交流合作,让学生利用自己已有的知识,在独立思考与交流合作中进行更深入的探究,使学生在亲自经历整个探究过程后,能够更深入的理解和掌握三角形的概念及三边的关系,并获得数学活动的经验,提高探究、发现和创新的能力.
中考 高考名著
常用成语