平行线及平行公理教学设计方案（二） 人教课标七年级下册

目标：

1、使学生掌握平行线的定义、画法和符号表示；

2、掌握平行公理及其推论

重点：平行的定义和平行公理及其推论

难点：理解平行的概念

教学过程：

一、复习提问

1、什么叫做三线八角?（同位角、内错角、同旁内角是如何形成的?）

2、如何才能正确地在一个图形中找出此三类角?关键是找什么?

3、如图，找出图中∠9的同位角、内错角、同旁内角。

二、新课学习

（一）自学检查

请几个同学说说本节课主要讲了哪些内容?

（平行线的定义、记法、画法，平行公理及其推论）

（二）提问

1、怎样的线是平行线?

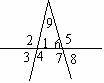2、平行线的形成有一个前提，是什么?没有这个前形不形?为什么?平行用什么符号表示?

3、在同一个平面内两条直线的位置关系有几种?

4、不相交的直线是不是一定是平行线?

5、如何画平行线?

（三）重点讲解

1、我们在讲平行线时一定要注意， 这是指在同一个平面内的不相交的两条直线。因此在同一个平面内，两条直线的位置关系只有相交和平行两种，垂直是相交的一种特殊情形。（不考虑重合）

2、在空间里存在着既不相交也不平行的直线，叫做异面直线。（举例说明）

3、要注意平行线是直线是无限延伸的，无论怎样延伸都不会相交，这样的直线才是平行线，同学们判断一下，如图是不是平行线?为什么?

4、如果说两条线段或射线平行，指的是它们所在的直线平行

5、平行用符号“∥”表示，注意是两撇，如AB∥CD，a∥b

6、当我们要画平行线时，一定要用块尺子，其中至少有一块是三角板。（师示范，可问为什么这样画的就是平行线?）

7、平行公理，是我们学习过的第三个公理（前两个是直线公理、线段公理），要注意其内容与垂线的性质很相似。

8、要注意平行公理的推论：如果两条直线都和第三条直线平行，则这两条直线也互相平行。用几何语言表示：

∵a∥b，b∥c ∴a∥c

课本在说明这个推论时（要求记下来），不是直线说明它们为什么会平行，而是假设它们相交，得到一个与已知或公理等矛盾的结论。这种方法大家其实也经常用，如代数我们规定：am÷an=am－n（a≠0），我曾经问过为什么a≠0，很多同学在回答时，不正面回答为什么a≠0，而是假设a＝0，从而得出在除法中失去意义。

（四）讲评练习：p70

三、小结：1、平行线定义、表示、画法；2、平行公理及推论