平行线及判定 教学设计

§5.2平行线及判定

教材分析

本节课是在上节课的基础上研究平面内两条直线位置关系中的另一种情形---------平行，这一节的主要内容是平行线的概念、平行公理及推论以及平行线的判定方法。这部分内容学生在前两个学段已有所接触，学生对平行线已有了直观地认识，因此，本节课是在学生已有知识和经验的基础上，来系统地研究平面内两条直线平行的情形。

平行线的判定是图形与几何领域的基础知识，是本节课的重点内容，在今后的学习中要经常用到，这部分内容掌握不好会影响后续内容的学习，学好这部分的关键是使学生理解与相交线、平行线有关的角的知识，因为直线的位置关系是通过有关角的知识反映出来的；在本节课中，除了让学生重点掌握以上的基础知识外，还应通过大量的识图和作图训练，来培养学生的图形感，同时，还应在解决问题的过程中注意学生推理能力的培养，这也是教学的难点。

【课时分配】2课时

§5.2.1平行线

【教学重点与难点】

教学重点：探索和掌握平行公理及其推论.

教学难点：理解平行线的概念以及由平行公理导出其推论的过程

【教学目标】

1、了解平行线的概念、平面内两条直线的相交和平行的两种位置关系， 知道平行公理以及平行公理的推论。

2、会用符号语方表示平行公理推论,，会用三角尺和直尺过已知直线外一点画这条直线的平行线。

3、经历观察教具模式的演示和通过画图等操作,交流归纳与活动,进一步发展空间观念。毛

【教学方法】

通过创设情境，以问题为载体给学生提供探索的空间，引导学生积极探索。教学环节的设计与展开，都以问题的解决为中心，使教学过程成为在教师指导下学生的一种自主探索的学习活动过程，在探索中形成自己的观点。

【教学过程】

一、创设情境 引入新课

（设计说明：利用直观教具动态演示并提出简单的问题，吸引学生的注意力，激发学生自主学习的兴趣和积极性。并自然引入新课。）

分别将木条a、b与木条c钉在一起，做成图所示的教具。

出示教具提出问题：

问题：把三根木条想象成三条无限延伸的直线，转动b，直线

b从在直线c的左侧与直线a相交逐步变为在右侧与直线a

相交的过程中（演示转动过程），你觉得直线a与直线b有

几种不同的位置关系?你是根据什么来区分这几种不同位置

关系的?

教师组织学生交流并形成共识：

顺时针转动b时,直线b与a的交点从在直线a上A点向左边距离A点很远的点逐步接近A点,并垂合于A点,然后交点变为在A点的右边,逐步远离A点.继续转动下去,b与a 的交点就会从A点的左边又转动A点的左边……在这一过程中大部分情况下直线b与直线a都有交点，但可以想象一定还存在一个直线b的位置，它与直线a左右两旁都没有交点；因此直线a与b交点的情况，可得出直线a与b有两种不同的位置关系： 相交或不相交，两直线相交前面我们已经学习过，这节课我们就来研究两条直线不相交的情形。由此引入新课

（教学说明：利用这一教具动态演示，可让学生感受到直线b从在直线c左侧与直线a相交逐步变为在右侧与直线a相交，中间存在一个两者不相交的位置，这样可以帮助学生直观理解平行线的概念，同时也让学生感受到了无论直线b转动几圈，直线b与直线a只有两种不同的位置关系，这就为学生理解同一平面内两直线的位置关系作了充分的准备。）

二、探索新知 解决问题

（一）、平行线

（设计说明：在引入的基础上，自然引导学生直接归纳出平行的概念以及同一平面内两直线的位置关系）

1、结合演示的结论,师生用数学语言描述平行定义：

同一平面内，存在一条直线a与直线b不相交的位置，这时直线a与b互相平行。

换言之，同一平面内， 不相交的两条直线叫做平行线。

直线a与b平行，记作“a∥b”,这里“∥”是平行符号。

2、同一平面内,两条直线的位置关系

问题：在同一平面内,两条直线有几种位置关系?

根据引入问题的分析学生不难得出：相交或平行

教师可引导学生明确：在同一平面内,根据两条直线的交点情况去确定两条直线的位置关系，即两条直线有一个交点时相交，没有交点时平行。

（教学说明：在教学过程中，要给学生充分的发言权，这样不仅可以锻炼学生的语言表达能力，还可以从学生的发言中发现学生的缺失，从而及时进行弥补；对于两个问题中为什么都有“在同一平面内”这一条件，可以让学生思考并进行解释，让学生认识平面几何与立体几何不同的同时，培养学生思维的严谨性。还要向学生说明，我们所说的两条直线，是指不重合的两条直线）

（二）、平行公理及平行公理推论

（设计说明：通过问题、画图、类比学习来引导学生探究平行公理及推论）

1、问题：在转动教具木条b的过程中，有几个位置能使b与a平行?

本问题学生凭直觉能认识到直线b绕直线a外一点B转动时，只有一个位置使a与b平行。

2、问题：如何用直线和三角尺画平行线?

引导学生回忆并总结出画平行线方法：

一“落”（三角板的一边落在已知直线上），二“靠”（用直尺紧靠三角板的另一边），三“移”（沿直尺移动三角板，直至落在已知直线上的三角板的一边经过已知点），四“画”（沿三角板过已知点的边画直线）．

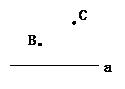已知：直线a，点B，点C

(1)过点B画直线a的平行线，能画几条?

(2)过点C画直线a的平行线，它与过点B的平行线平行吗?

3、通过观察画图、归纳平行公理及推论

(1)由学生对照垂线的第一性质说出画图所得的结论。

(2)在学生充分交流后，教师板书。

平行公理：经过直线外一点,有且只有一条直线与这条直线平行。

(3)比较平行公理和垂线的第一条性质。

共同点：都是“有且只有一条直线”，这表明与已知直线平行或垂直的直线存在并且是唯一的。

不同点：平行公理中所过的“一点”要在已知直线外，二垂线性质中对“一点”没有限制，可在直线上，也可在直线外。

4、归纳平行公理推论

(1)学生直观判定过B点、C点的a的平行线b、c是互相平行的。

(2)从直线b、c产生的过程说明直线b∥直线c。

(3)学生用三角尺与直尺用平推方验证b∥c。

(4)引导学生用数学语言表达这个结论，教师板书。

结论：两条直线都与第三条直线平行，那么这条直线也互相平行。

结合图形，教师引导学生用符号语言表达平行公理推论：

如果b∥a，c∥a

那么b∥c

(5)初步应用

练习：如果多于两条直线,，比如三条直线a、b、c与直线L都平行, 那么这三条直线互相平行吗?请说明理由。

（教学说明：借助于引入中的模型来引入平行公理，使学生对平行公理有一个初步的感知，进而通过画图验证，类比总结得出平行公理，使学生对平行公理的认识由感性上升到理性，同时在这一过程中也培养了学生善于类比的思想和学生语言的规范性。平行线的画法是几何画图的基本技能之一，在以后的学习中，会经常遇到画平行线的问题，画图时要使用工具，不能徒手画，因此在画图之前先引导学生回顾了平行线的画法，为学生下面的画图探究做好准备。平行公理的推论是今后证明两直线平行的方法之一，因此让学生用符号语言表示可培养学生的符号感，为今后的推理做准备，初步应用练习让学生在反复运用平行公理推论中掌握平行公理推论以及说理的规范性。）

三、巩固训练 熟练技能

（设计说明：通过形式不同的练习加强学生对知识的理解，训练学生灵活应用知识解决问题的能力）

一、填空题.

1、在同一平面内，两条直线的位置关系有_________。

2、在同一平面内，一条直线和两条平行线中一条直线相交，那么这条直线与平行线中的另一边必__________。

3、同一平面内，两条相交直线不可能与第三条直线都平行，这是因为________。

4、两条直线相交，交点的个数是________，两条直线平行,交点的个数是_____个。

二、判断题.

1、不相交的两条直线叫做平行线。( )

2、如果一条直线与两条平行线中的一条直线平行, 那么它与另一条直线也互相平行。( )

3、过一点有且只有一条直线平行于已知直线。( )

三、解答题.

1、读下列语句，并画出图形后判断。

(1)直线a、b互相垂直，点p是直线a、b外一点，过p点的直线c垂直于直线b。

(2)判断直线a、c的位置关系，并借助于三角尺、直尺验证。

2、试说明三条直线的交点情况，进而判定在同一平面内三条直线的位置情况。

答案:

一、1.相交与平等两种 2.相交 3.过直线外一点有且只有一条直线与已知直线平行 4.一个,零

二、1.× 2.∨ 3.× 三、1.(1)略 (2)a∥c 2. 交点有四种,第一没有交点,这时第三条直线互相平行,第二有一个交点,这时三条直线交于同一点,第三有两个交点,这时是两条平行线与第三条直线都相交,第四有三个交点,这时三条直线两两相交.毛

（教学说明：在解决问题的过程中，要注意让学生说明解决问题的依据，从而培养学生的说理能力和解决问题有依有据的良好习惯；关注学生作图能力和规范性。）

四、总结反思，情意发展

（设计说明：设计了以下三个问题，让学生围绕这三个问题，先反悟，后谈自身的收获和疑问，最后师生共同归纳总结）

1.本节课你认为自己解决的最好的问题是什么?

2.本节课你有哪些收获?

3.在本节课的学习中，你还存在哪些疑问?

（教学说明：通过对以上三个问题的思考引导学生回顾整节课的学习历程，让学生对知识有一个沉淀、吸收的过程。此外，由于学生的学习基础、反思归纳能力不同，所以不同的学生可能会有不同的收获，学生之间的这种差异也是一种学习资源。通过教师为学生提供的交流互动的平台，使学生倾听别人的想法、意见、收获的同时，不断完善自己的认识，形成完整的知识结构.）

五、课堂小结

1．本节主要学习了平行线的意义、表示方法和平性线的两条性质.

2．主要用到的思想方法是类比法

3．注意的问题平行线的画法

六、布置课后作业：

课本18页习题11

七、拓展延伸

探究：

（1）、点D是△ABC中AB边上的中点。①过点D作BC的平行线，交AC于E。②量一量AE、CE的长度，它们相等吗?③量一量DE、BC的长度，它们有何关系?

（2）、在梯形ABCD中，AD∥BC，点E是AB的中点。①过点E作AD的平行线，交CD于点F，EF与BC平行吗?②量一量DF、CF的长度，它们相等吗?③量一量EF、AD、BC的长度，它们有何关系?

（教学说明：通过这组练习，既复习了平行线的画法及平行公理的推论，又以探究的形式将知识进一步延伸，拓广了学生的思维，同时为以后学习三角形和梯形的中位线定理埋下了伏笔。）

【评价与反思】

在本节课的教学中关注概念的形成过程，借助于直观形象的教具让学生充分的理解概念，通过动手实践、小组讨论给学生提供了探索、交流的空间，使教学活动不是单纯的依赖模仿与记忆，而是一个生动活泼、积极主动和富有个性的过程。

在学习过程中，采用了类比学习的方法，这不仅使学生自然的接受新知识，同时又对比出了相近知识的不同之处，也让学生学会学习的方法，培养学生可持续学习的能力。