可化为一元一次方程的分式方程及其应用3人教课标八年级下册

一、教学过程

(一)复习提问

1．什么是方程，什么是方程组?什么是方程的解，什么是方程组的解?

答：方程就是含有未知数的等式．使方程左右两边相等的未知数的值叫做方程的解．使方程组的每一个方程左右两边都相等的未知数的值，叫做方程组的解．

2．解分式方程的主要思想和一般解法是什么?

答：解分式方程的主要思想是化分式方程为整式方程，一般方法是将方程两边同乘最简公分母去分母，化分式方程为整式方程．

(二)新课

分析：如何处理-x2-x-1是解题的关键．把-x2-x-1看作一个整体-(x2＋x＋1)会使计算简便．

解：方程两边都乘以(x-1)，得

x3-(x-1)(x2＋x＋1)=x-1

x3-(x3-1)=x-1

x=2．

检验：把x=2代入分式方程分母中不为零．

∴ x=2是原方程的解．

小结：在本题中我们可以看到把-x2-x-1看作一个整体，有了这种整体思想，灵活去分母问题就会变得简单多了．

分析：

(1)对于这个方程如果要用一般的去分母方法，就要两边同乘以(x-1)(x-2)(x-3)(x-4)，而乘完之后每一项都会出现三个式子相乘如(x-1)(x-2)(x-3)，对于这样的解法计算量很大，很麻烦．

解法一：

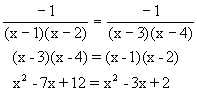
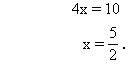
解法二：

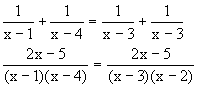
(分母不等，分子相同，则分子必为0)

检验：(同上)

小结：类似这样的方程，先通分再去分母，这样灵活去分母会使解题过程变得简单．

分析：

提问：这个题和上一个题有什么相似之处，有什么联系?

易化成分子是1的分式，从而转化成上一例题那种类型题．

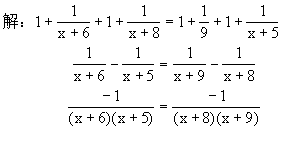
(x＋8)(x＋9)=(x＋6)(x＋5)

x2＋17x＋72=x2＋11x＋30

6x=42

x=-7．

检验：把x=-7分别代入原方程各分母，均不为零．

∴ x=-7为原方程的解．

小结：在解这个方程的过程中渗透着由未知到已知的数学转化思想．

例4 解方程组

分析：解分式方程的基本思想是化分式方程为整式方程，而解含有分式方程的方程组也需要把分式方程化为整式方程．

解：(1)式化简得：2x-y=10．

(2)式化简得：x＋y=-1．

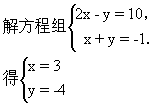
例5 解方程组

解：(1)式化简得：12y＋12x=xy．

(2)式化简得：80y-30x=3xy．

这是二元二次方程组，目前还不会解．

可以把原方程改写为

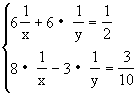
个方程组就转化为一个关于A、B的二元一次方程组了．

法．

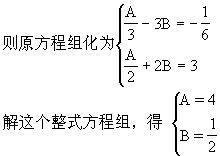
解这个整式方程组，得

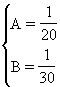
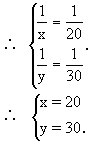
而且把未知数由x、y换成A、B了，所以叫换元法．换元法是非常有用而且非常重要的数学方法．

(三)练习

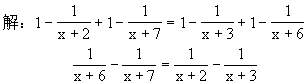
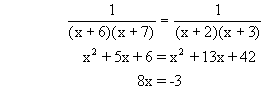
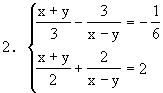
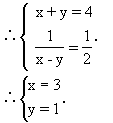
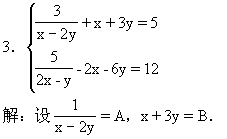
则原方程化为

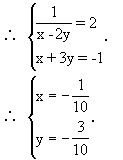
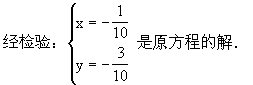
(四)小结

1．在解分式方程中应会灵活去分母．

2．换元法是非常重要的方法，可以使问题化简．

二、作业

教材p．107中8；p．108中9；p．108中B3、4．

三、板书设计