分式的加减法4 人教课标八年级下册

教学过程

(一)请学生纠正作业中的计算问题

(二)新课

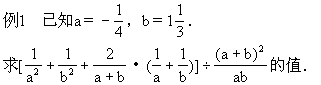
解：

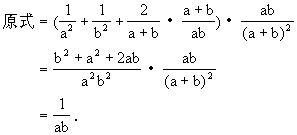
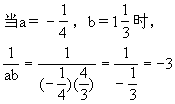
小结：先化简再求值是求所有代数式值的一般原则．

解：变形条件，代入代数式

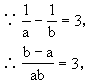
∴b-a＝3ab．

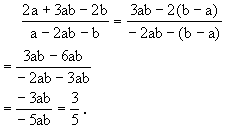
小结：

1．这是条件求值问题，即适当的对条件或结论作恒等变形，然后再把条件代到结论中去，最终达到求代数式值的目的．一般地说，这种变形有以下三种情况：适当地变条件；适当地变结论；同时变条件与结论．

2．将b-a＝3ab代入代数式的方法一般称为“整体代入法”，这也是代数运算中的一种常用方法．

练习：

(1)已知：x²-3x＋1＝0．

解：∵x²-3x＋1＝0，

∴x²＋1＝3x．

由题目隐含条件：x≠0．

∴两边同除以x，得：

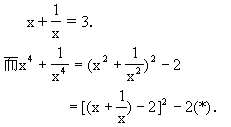
［3²-2］²-2

=(9-2)²-2

=49-2=47．

(2)记知：6x²＋12y²＝17xy．

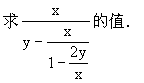
解：

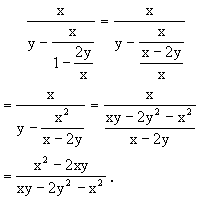
∵6x²＋12y²＝17xy

∴6x²-17xy＋12y²＝0

(2x-3y)(3x-4y)＝0

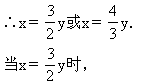
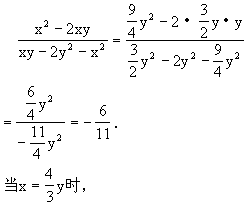
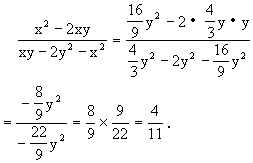
例2 把下列各式化为整式部分与分式部分的和．

分析：类比假分数化带分数的过程，提出分式可否化为整式部分与分式部分的和的形式的问题，由学生思考讨论并找出解决方法．

解：由多项式除法

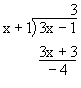
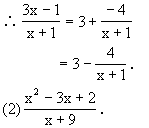
解：

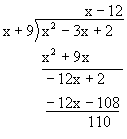
小结：如同假分数化为带分数一样，有时将一个分式化成整式部分与分式部分的和可以使计算简化．

(三)课堂小结

1．条件求值问题．

2．把一个分式化为整武部分与分式部分的和的方法．

作业

教材p.86中3、4、5．

补充：思考题：

求a、b．

板书设计