分式的乘除法 人教课标八年级下册

教材分析：

分式的乘除法是本章的一个重要的内容，是分式的基本性质、分式的约分的进步提高及应用。本课时包含分式的乘法、分式的除法、分式的乘方三部分内容。分式的除法、分式的乘方都可以转化为分式的乘法进行运算。分式的乘法是本课时的一个重点。分式的乘除法是建立在小学分数运算的基础上，又与数的运算有很大的不同。

教学目标：

（一）知识与技能目标：

使学生理解并掌握分式的乘除法、乘方运算方法，能进行简单的分式乘除法、乘方运算，能解决一些与分式乘除有关的实际问题；

（二）数学思考目标：

经历探索分式的乘除法、乘方运算方法，发展合情推理的推理能力，培养学生大胆猜想的能力；

（三）解决问题能力：

形成解决问题的基本策略，从特殊到一般，从分数的乘除法运算到分式的乘除法运算，也为以后学习分式的加减运算作铺垫；

（四）情感与价值目标：

教学中注意渗透类比转化思想，让学生在大胆猜想中学到方法，培养学习数学的自信心。

教学重点：

使学生掌握分式的乘除法运算。

教学难点：

分子、分母为多项式的分式的乘除法运算，分式的乘方运算。

教学方法：

探究式、小组交流合作。

学生分析：

学生前面已学习了分式的基本性质、分式的约分，对学好本课时内容有一定的帮助。九年级学生有一定逻辑推理能力、代数式的运算的能力，主动探索知识的学风也初步形成。但数与式的差别也制约着学生的学习，特别是分子、分母为多项式的乘除法运算是学生学习的一个难点。

教学过程：

一、提出问题：

上海到北京的航线全程为s千米，飞行时间需a小时；铁路全长为航线长的m倍，乘车时间需b小时。飞机的速度是火车速度的多少倍?（用含a、b、s、m的分式表示）

学生小组讨论，列式：

提问：这是一个什么运算?怎样计算呢?

（板书课题：§21.3 分式的运算 1、分式的乘除法）

二、探索新知：

（旧知再现）计算：

学生交流：分数乘法法则?分数除法法则?

（大屏幕展示）：

分数乘法法则：分数乘以分数，用分子的积做积的分子，分母的积做积的分母。

分数除法法则：分数除以分数，把除数的分子和分母颠倒位置后，再和被除数相乘。

第（3）小题可先约分再相乘。第（4）小题，先把除法化为乘法，然后约分、相乘。

探索新知：

你能用代数式表示上题中（1）、（2）的计算过程中吗?与同伴交流。

经观察类比，不难发现：

你能归纳出分式乘法、除法法则吗?

(大屏幕显示，把分数的运算法则中，“数”改为“式”即可)

分式乘法法则：分式乘以分式，用分子的积做积的分子，分母的积做积的分母。

分式除法法则：分式除以分式，把除式的分子和分母颠倒位置后，再和被除式相乘。

通过类比，得出：①分式乘除法与分数乘除法类似；②“数”变为“式”后，其运算又有不同。

(3)解决课前提出的问题：

学生板演：

三、范例学习：

例1计算：

(1) (2)

注意：（1）运算的步骤：(1)小题先乘后约分或先约分后乘；(2)小题先把除法化为乘法，再按乘法法则进行计算；

（2）分式运算的结果通常要化为最简分式或整式。

例2 计算：

引导学生分析：

（1）与例1的区别，分子分母为多项式；

（2）能不能直接约分??统一认识：约分是约去分子与分母的公因式，而x不是因式，所以不能这样约分；

（3）解题步骤：先将分子与分母分解因式，再约分，最后相乘。

（4）分式运算的结果通常要化为最简分式或整式。

四、探索分式的乘方。（小组交流）

（练习）计算：

（1） （2）

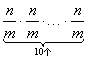
思考：这两个算式能不能用乘方表示?与结果比较你能发现什么规律?

可得：，

猜想： （）

分式的乘方，等于分子分母各自乘方。

五、课堂练习：

下列计算是否正确，如有错误，请改正。

（正确答案：）

p9，第1、2题（学生板演，小组内交换检查）

六、小结

通过本节课学习，你学到了哪些知识和数学思想?

分式的乘法、除法、乘方；

了解数学中重要的一种思想——类比转化思想，由小学所学分数的乘除法类比到分式的乘除法，分式的除法、乘方都可以化归为分式的乘法。

七、作业

p11 习题21.3 第1题；p12 第5题。

教学反思：

本节课由问题开始，使学生明白数学来源于生活，让学生养成学数学、用数学的习惯。本节课围绕分式的乘法运算来进行教学，重点突出。通过与分数乘除法运算类比，使学生较易掌握本节内容。难点通过举反例的形式，使学生掌握正确的运算方法、运算顺序。

不足之处：内容较多，学生探究的时间不够充分。