不等式与不等式组教材分析

第九章 不等式与不等式组

【本章教材分析】

1．内容结构特点

本章首先以实际问题为例，结合问题中的不等关系，引出不等式及其解集的概念；然后类比一元一次方程，引出一元一次不等式的概念．为进一步讨论不等式的解法，教科书接着对不等式的性质进行了讨论，得出不等式的三个性质，并运用它们解简单的不等式．不等式的性质是解不等式的重要依据；然后，从一个选择购物商店问题入手，对列、解一元一次不等式作进一步的讨论，结合三角形三条边的大小关系，引进了一元一次不等式组及其解集的概念，并对一元一次不等式组的解法进行了探索。

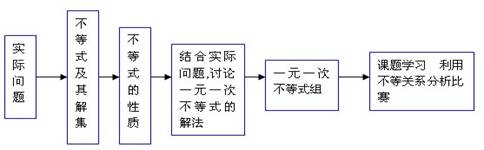
2．知识结构图

3．教材的地位及作用

本章是在研究方程的基础上，对刻画现实世界数量关系的重要模型——不等式（组）的研究，是数学在现实生活中的具体应用，它为实际问题数学化提供了模型化，它在数学中具有承上启下的作用。

3．教学重点和教学难点

教学重点：以不等式（组）为工具分析问题、解决问题

教学难点：不等式（组）在实际中的应用

4．教学目标

（1）了解一元一次不等式及其相关概念，经历“把实际问题抽象为不等式”的过程，能够“列出不等式或不等式组表示问题中的不等关系”，体会不等式（组）是刻画现实世界中不等关系的一种有效的数学模型．

（2）通过观察、对比和归纳，探索不等式的性质，能利用它们探究一元一次不等式的解法．

（3）了解解一元一次不等式的基本目标（使不等式逐步转化为 的形式），熟悉解一元一次不等式的一般步骤，掌握一元一次不等式的解法，并能在数轴上表示出解集，体会解法中蕴涵的化归思想．

（4）了解不等式组及其相关概念，会解由两个一元一次不等式组成的不等式组，并会用数轴确定解集．

（5）通过课题学习，以体育比赛问题为载体，探究实际问题中的不等关系，进一步体会利用不等式解决问题的基本过程（见上图），感受数学的应用价值，提高分析问题、解决问题的能力．

5．教学建议

（1）注重类比，做好从方程到不等式的迁移

从课程标准看，方程与不等式是同属“数与代数”领域内同一标题下的两部分内容，它们之间有密切的联系，存在许多可以进行类比的内容，充分发挥学习心理学中正向迁移的积极作用，借助已有的对方程的认识，可以为进一步学习不等式（组）提供一条合理的学习之路．

（2）突出数学建模思想，反映不等式（组）与实际问题的联系

实际问题中有许多涉及数量间的大小关系的比较，这为学习“不等式与不等式（组）”提供了大量的现实素材．在本章教科书中，实际问题情境贯穿于始终，对不等式解法的讨论也是在解决实际问题的过程中进行的，正如“列方程（组）”在前面有关方程的几章中占有突出地位，本章中“列不等式（组）”始终是重点内容，尽管数学模型的形式由方程（组）转变为不等式（组），数学建摸思想却在已有基础上得到进一步的发展和强化，利用不等式（组）解决实际问题的基本过程（见前面的图），在本章中的小结中出现，它与前面方程（组）在这方面的框图的基本结构一致，这有助于从整体上进一步加强对数学模型与实际问题关系的认识，在教学、学习和复习时应注意不断强化对它的认识．

（3）重视数学思想方法的渗透

本章所涉及的数学思想方法主要包括两个：一个是由实际问题抽象为不等式（组）这个过程中蕴涵的符号化、模型化的思想；另一个是解不等式（组）的过程中蕴涵的化归思想．前面有关方程（组）的章节中对这些思想方法已多次进行渗透，本章中讨论的对象为一元一次不等式（组），最终要使不等式（组）变形为x>a或x

此外，充分利用数轴对于解不等式组是行之有效的方法，在本章的教学和学习中，应体现数学中数形结合的研究方法，使学生认识到借助直观思考问题的优越性，这对后续学习是有益的．

（4）关注基础知识和基本技能

本章内容包括一元一次不等式（组）的概念、解法和应用．一元一次不等式是最基本的代数不等式，对它的理解和掌握对于后续学习（其他的不等式以及函数等）具有重要的基础作用．因此，教学和学习中应注意打好基础，对本章中的基础知识和基本技能、能力等进行及时的归纳整理，安排必要的、适量的练习，使得学生对基础知识留下较深刻的印象，对基本技能达到一定的掌握程度，发展基本能力．

6．课时分配

9.1 不等式 2课时

9.2 实际问题与一元一次不等式 2课时

9.3一元一次不等式组 2课时

复习课 1课时