“同位角、内错角、同旁内角”教学设计

[教学目标]

1．能说出同位角、内错角和同旁内角的意义。

2．会识别图形（包括变式图形和比较复杂的图形）中的同位角、内错角和同旁内角。

此外，这种训练过程中，不断提高学生排除变式图形中的非本质现象。复杂图形中“背景”干扰的能力。

［引导性材料］

1．复习两条直线相交得到的四个角的位置关系及性质；

（在两条直线相交得到的四个角的位置及大小关系知识的基础上，进一步研究一条直线与两条直线相交得到的八个角的位置关系。）

2．展示图形，如图2．3—1，引导学生分析图中八个角的位置关系。

（帮助学生从直观上感知“同位”、“内错”、“同旁”等位置关系，为下面的新课学习作充分准备。）

图2．3－1

[知识产生和发展过程的教学设计]

问题1－1：如图2．3－1，怎样描述直线AB、CD和EF的位置关系?

（引导学生说出“直线AB、CD和EF相交”，或者“两条直线AB、CD被第三第直线EF所截”。）

问题1－2：如图2．3－1中，直线AB、CD被EF所截得到八个角，这其中有哪些我们已经学过的有特殊位置关系的角?

问题2－1：观察图2．3－1中的∠1和∠5，它们的位置关系有什么特点?

（引导学生观察得出这两个角分别在直线AB、CD的同一方（上方），并且都在直线EF的同一侧（右侧），这是“同位角”的本质属性。然后，可以用“位置相同”来描述这种位置关系，给出“同位角”的描述性定义。）

像这样位置相同的一对角叫做同位角。

问题2－2：你还能在图2．3－1中找出其他的同位角吗?一共有几对?

问题2－3：你能看出两个同位角的边与边之间有什么关系吗?

（互为同位角的两个角没有公共顶点和公共边，但有一条边在同一条直线上，然后将上述互为同位角的两个角，从图2．3－1中分解出来，画出如图2．3－2的草图，从这些简单图形中容易识别出∠1和∠2都是同位角。可顺便指出，形如“F”的图形中有同位角。）

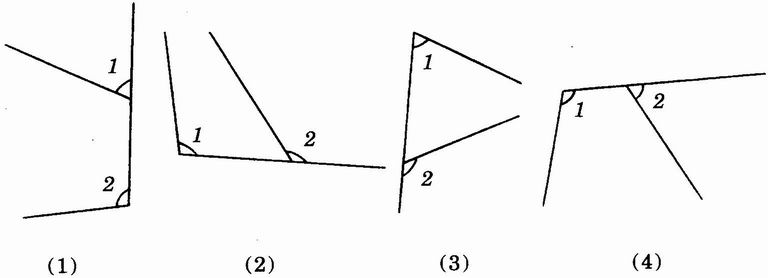
图2．3－2

这就是把复杂图形“分解”为简单图形的训练，这种训练能有效地帮助学生掌握识图技能，从而扫除学生识别内错角、同旁内角时可能存在的障碍。

此外，还要训练学生用规范的几何语言描述；如图2．3－1中，∠1和∠5是“直线AB和直线CD被直线EF所截得的“同位角”。

问题2－4：图2．3－3中的∠1和∠2是同位角吗?为什么?

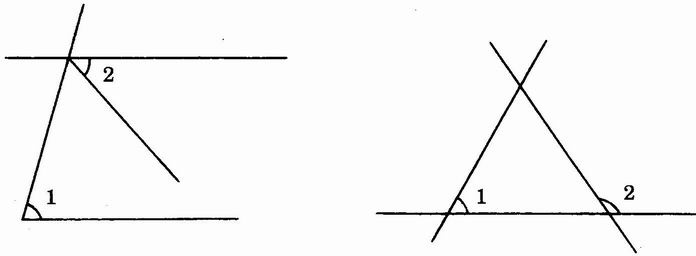
图2．3－3

（本题考察学生是否理解“同位角”的意义（本质属性）以及对变式图形的识别能力。

以上关于“同位角”的内容，应作为本课的重点，以便“举一反三”。）

问题3－1：图2．3－1中的∠3和∠5的位置关系是怎样的?

（在分析同位角的基础上，学生较容易能得出∠3和∠5在直线AB、CD之间，并且分别在直线EF的两侧。“像这样的一对角叫做内错角”。其中“错”为“交错”的意思。）

问题3－2：图2．3—l中还有哪些角是内错角?

问题3－3：你会从图2．3－1中“分解”出这些内错角吗?这些（分解后的内错角）图形像哪一个英文字母?

（训练学生分解图形的技能，并可引导学生得出“Z”形图形的两个角是内错角。

要求学生说出图2．3－l中的内错角是哪两条直线被哪一条直线截得的。）

问题3－4：图2．3－4中的∠1和∠2是内错角吗?为什么?

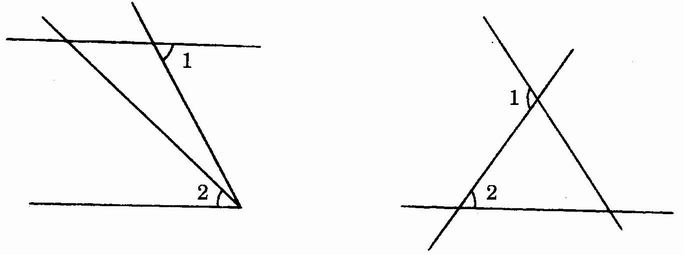
图2．3－4

问题4－1：观察图2．3－1中的∠4和∠5有什么位置关系?

∠4和∠5都在直线AB、CD之间，但它们在直线EF的同一侧，像这样的一对角叫同旁内角。

问题4－2：图2．3－1中还有哪些同旁内角?并说出它们是哪两条直线被哪一条直线截得的?

（进而仿照教学同位角和内错角的过程，进行相应的识图和语言叙述的训练。）

问题4－3：图2．3－5中的∠1和∠2是同旁内角吗?为什么?

[例题讲解]

课本第68页例题。

（本例题既考查了对基本图形的识别，又考查了对学过的“对顶角”和“邻补角”等知识的掌握及运用。）

[练习]

课本第68页练习第1、2题．

（第2题主要考查学生对变式图形的识别能力，如果学生仍有困难，教学中应引导学生回到定义，抓住本质去识别同位角、内错角和同旁内角。）

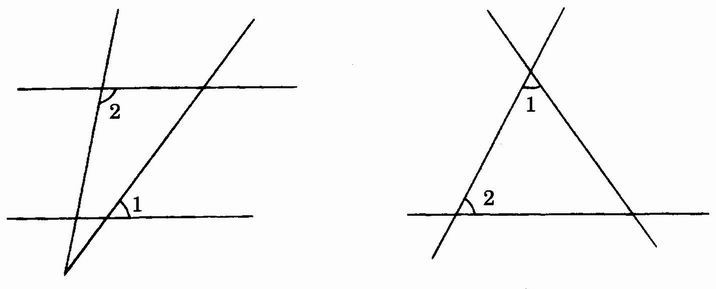
图2．3－5

[小结]

本节课学习了两条直线与第三条直线相交所得八个角的有关知识，重点训练和培养学生对复杂图形和变式图形的识别能力。

[作业]

课本第71页习题2．1A组第9、10题；B组第1题可组织学有余力的同学讨论。